Introdução à ordenação

Nesta seção examinaremos os algoritmos mais básicos para ordenação de uma lista de dados (vetores). Os algoritmos examinados aqui não são eficientes e por isso para aplicações reais usualmente são implementados outros (como Ordenação Rápida/Quick Sort, Ordenação por Fusão/Merge Sort ou Ordenação por Monte/Heap Sort). O último a ser examinado (Inserção), é mais eficiente, principalmente se os dados estiverem "quase-ordenados".

O problema é, dada uma sequência de valores (em lista ou vetor), ordenar crescente (ou decrescente) essa sequência. Por exemplo, na figura abaixo, inicialmente os dados não estão ordenados {4, 2, 3, 0, 9, 3, 5, 7}. Um algoritmo de ordenação que recebesse esse vetor com n=8 valores, deveria trocar os valores de posição de modo a conseguir a seguinte situação final para o vetor: {0, 2, 3, 3, 4, 5, 7, 9}.

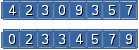
Fig. 1. Ilustração dos dados na configuração inicial e na final (já ordenado V[0]<V[1]<...<V[n-1]).
 

Para simplificar as explicações fixaremos um nome para o vetor e usaremos a notação V[i] para indicar o valor que está na posição i do vetor. Também convencionaremos que a primeira posição do vetor seja V[0], logo um vetor com N elementos terá o último deles na posição V[N-1].

Os métodos que examinaremos são os conhecidos: Método da Bolha (Buble Sort), Seleção Direta e Inserção Direta.

A ideia do método da Bolha é inicia comparando os dois últimos elementos, o menor fica à esquerda, então comparar os dois anteriores e fazer a mesma coisa, desse modo o menor vai movendo-se para cima (como as bolhas). Mas também podemos fazer o "inverso", seguir empurrando o maior para baixo e assim, poderíamos apelidar essa variante de método do Pedregulho.

Vamos detalhar a primeira fase do método do Pedregulho, nessa fase empurramos o maior do N elementos para a última posição. O primeiro passo é comparar V[0] com V[1], se o valor em V[0] for maior que o valor em V[1], troque seus valores (diremos apenas Se (V[0] > V[1], troque-os). O passo 2 é: Se (V[1] > V[2], troque-os (logo V[2] terá o maior dos 3 primeiros). O passo 3 é: Se (V[2] > V[3], troque-os (logo V[3] terá o maior dos 4 primeiros). Segue comparando V[i] com V[i+1], até o passo N-1: Se (V[N-2] > V[N-1], troque-os (logo V[N-1] terá o maior dos 4 primeiros).

A figura abaixo ilustra os 7 primeiros passos, na etapa 1, do algoritmo para levar o maior elemento (considerando N=8) para a posição 8.

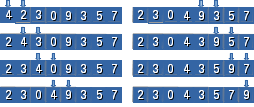
Fig. 2. Ilustração do Método do Pedregulho, coluna da esquerda as quatro primeiras "descida" do tipo V[i]<V[i+1].

Note que na primeira imagem (acima, esquerda), existem os 8 na ordem inicial {4, 2, 3, 0, 9, 3, 5, 7}. Cada passo de comparação dos pares de vizinhos está indicado por duas setas sobre os valores a serem comparados. Na representação seguinte, o vetor é novamente apresentado, eventualmente tendo sido trocados os (se V[i]>V[i+1]). Na passo 7, usamos apenas uma seta para indicar que o maior dentre todos os elementos foi para a última posição.

Mas, como o objetivo é ordenar, não apenas descobrir o maior, podemos usar a mesma ideia (de modo indutivo): aplica-se o mesmo algoritmo (empurrar o maior para a última posição), mas considerando agora apenas os 7 primeiro elementos, pois o maior já está na posição 8. Novamente, isso resultará no segundo maior na posição 7

Mais uma vez (em geral) o vetor não está ordenado, mas podemos aplicar a mesma ideia mas 5 vezes: para V[0]..V[6] (maior deles para V[6]); para V[0]..V[5] (maior deles para V[6]); para V[0]..V[4] (maior deles para V[6]); para V[0]..V[3] (maior deles para V[6]); para V[0]..V[2] (maior deles para V[6]); para V[0]..V[1] (maior deles para V[1]).

Desse modo obtém-se o vetor em ordem crescente! Abaixo apresentamos o algoritmo do Pedregulho (Bolha) em C e em Python.

// Ordena bolha/pedregulho
#include <stdio.h>
void imprimir (int X[], int n) {
  int i;
  printf("(");
  for (i=0; i<n; i++) printf("%3d ", X[i]);
  printf(")\n");
  }
void ordPedregulho (int V[], int n) {
  int i, j, aux;
  for (i=0; i<n; i++)
    for (j=0; j<n-i-1; j++)
      if (V[j]>V[j+1]) { // troque-os
        aux = V[j]; // presevar V[j]
        V[j] = V[j+1];
        V[j+1] = aux; }
  }
int main (void) {
  int Y[] = { 4, 2, 3, 0, 9, 3, 5, 7 }; // definir vetor dados
  imprimir(Y, 8);
  ordPedregulho(Y, 8);
  imprimir(Y, 8);
  }
   

# Ordena bolha/pedregulho
from __future__ import print_function; # imprime sem mudar linha Python 2
def imprimir (X, n) :
  print("(", end="");
  for i in range(n) :
    print("%3d " % X[i], end="");
  print(")");

def ordPedregulho (V, n) :
  for i in range(n) :
    for j in range(n-i-1) :
      if (V[j]>V[j+1]) : # troque-os
        aux = V[j]; # preservar V[j]
        V[j] = V[j+1];
        V[j+1] = aux;

def main () :
  V = [4, 2, 3, 0, 9, 3, 5, 7]; # definir vetor dados 
  imprimir(V,8);
  ordPedregulho(V, 8);
  imprimir(V,8);

main();

A ideia o método da Seleção Direta é novamente deixar na última posição o maior elemento (ou o menor na primeira), mas diferentemente do método da Bolha, nesse mantém-se fixado o último elemento, comparando-o com o primeiro, com o segundo e assim por diante. Considerando novamente um vetor com 8 elementos, após 7 comparações (e eventuais trocas), o maior deles estará na posição 8.

Esse método está ilustrado na figura abaixo. Na primeira coluna estão os 7 passos para obter o maior elemento em V[7]. Na coluna 2 estão os 6 passos para obter o segundo maior para V[6]. Na coluna 3 estão os 5 passos para obter o terceiro maior para V[5] e na coluna 4 estão os 4 passos para obter o quarto maior para V[6]. Para finalizar o algoritmo deve-se fazer mais duas sequências de passos (ou laços), fixando-se o elemento 3 para obter o 5-ésimo (5=8-3) maior e fixando-se o elemento 2 para obter o 6-ésimo (6=8-2) maior.

Fig. 3. Ilustração do Método da Seleção Direta, coluna da esquerda os primeiros passos (na etapa 1), resultando em V[i]<V[n-1], i<n-1 (n=8).
 

Abaixo está uma implementação do método Seleção Direta em C e em Python.

// Ordena Selecao Direta
#include <stdio.h>
void imprimir (int X[], int n) {
  int i;
  printf("(");
  for (i=0; i<n; i++) printf("%3d ", X[i]);
  printf(")\n");
  }
void ordSelecao (int V[], int n) {
  int i, j, aux;
  for (i=n-1; i>0; i--)
    for (j=0; i<i; j++)
      if (V[j]>V[i]) { // troque-os
        aux = V[j]; // presevar V[j]
        V[j] = V[i];
        V[i] = aux;
        }
  }
int main (void) {
  int Y[] = { 4, 2, 3, 0, 9, 3, 5, 7 }; // definir vetor dados
  imprimir(Y, 8);
  ordSelecao(Y, 8);
  imprimir(Y, 8);
  }
   

# Ordena Selecao Direta
from __future__ import print_function; # imprime sem mudar linha Python 2
def imprimir (X, n) :
  print("(", end="");
  for i in range(n) : 
    print("%3d " % X[i], end="");
  printf(")");

def ordSelecao (V, n) :
  for i in range(n-1, 0, -1) :
    for j in range(i) :
      if (V[j]>V[i]) : # troque-os
        aux = V[j]; # preservar V[j]
        V[j] = V[i];
        V[i] = aux;

def main () :
  V = [4, 2, 3, 0, 9, 3, 5, 7]; # definir vetor dados 
  imprimir(V,8);
  ordSelecao(V, 8);
  imprimir(V,8);

main();

Note que os comandos para trocar os conteúdos entre V[j] e V[i] (subordinado ao if (V[j]>V[i])) poderia ser evitado, bastaria mais duas variáveis auxiliares, imax e max, respectivamente, para armazenar o índice do maior valor e o maior valor (max = V[imax]). Assim, ao final laço for j faríamos apenas uma troca (entre V[i] e V[imax]). Nessa variante do algoritmo, o número de passos e de comparações é o mesmo, entretanto o número de trocas (geralmente) seria bem menor!

A ideia o método da Inserção Direta é um pouco diferentes do Bolha e Seleção, naqueles após cada laço interno um elemento maior ficava em sua posição "definitiva", no Inserção não. A ideia do Inserção é (na etapa i de ordenação): suponha que V[0] até V[i-1] esteja ordenado, então podemos estender a ordem localizando o primeiro elemento, da direita para a esqueda, que não seja maior que V[i], digamos que seja o V[j], então move-se todos eles uma posição para a sua direita, abrindo a posição V[j] para inserir o V[i]. Esse princípio é ilustrado abaixo com j=3:

1. V[0]<V[1]<V[2] odernados; 2. V[3] libera seu espaço (cópia em aux); 3. todos os elementos com valor estritamente maior que aux "dão um passo para a direita"; 4. a posição i=0 é liberada para inserir ali aux (estendendo a ordenação para 4 elementos).

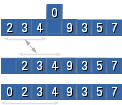
Fig. 4. Ilustração dos "deslocamentos" para inserir a chave (inicialmente) na posição V[3] para a posição correta (V[0]<V[1]<V[2]<V[3].

Esse método está ilustrado na figura abaixo. Na primeira coluna estão as 3 instruções para obter uma ordenação com os 2 primeiros elementos. Na coluna 2 estão as 4 instruções para obter ordenação dos 4 primeiros elementos e na coluna 3 estão as 5 instruções para obter ordenação dos 5 primeiros elementos.

Fig. 5. Ilustração do Inserção Direta: na primeira coluna representa a etapa 1 de ordenação a chave é o 2 na posição V[1]; na segunda a chave é o 0 na posição V[3].
 

É importante notar que se os dados estiverem já ordenados, serão realizadas apenas n=7 operações! De modo geral, se a etapa de ordenação i resultar em ordenação completa dos dados, deste ponto em diante, serão feitas apenas n-i-1 comparações e nenhuma troca (!). Pode-se usar uma bandeira para identificar tal fato e finalizar o algoritmo.
Por exemplo, na última coluna da figura 5, se o valor em V[4] fosse 5 (ou qualquer outro valor maior), haveria apenas três instruções (independe do valor 5): copiar V[3] para aux, comparar aux com V[2] e, como aux é maior (ou igual), finalizaria, copiando aux novamente para V[3].

Abaixo está uma implementação do método Inserção Direta em C e em Python.

// Ordena Insercao Direta
#include <stdio.h>
void imprimir (int X[], int n) {
  int i;
  printf("(");
  for (i=0; i<n; i++) printf("%3d ", X[i]);
  printf(")\n");
  }
void ordInsercao (int V[], int n) {
  int i, j, aux;
  for (i=1; i<n; i++) {
    aux = V[i]; // "abrir espaco" copiando V[i]
    j = i-1;
    while (j > -1 && V[j] > aux) { // mova para direita os maiores que aux
      V[j+1] = V[j]; // mover para direita V[j]
      j -= 1;
      }
    V[j+1] = aux; // coloque aux na posicao correta
    }
  }
int main (void) {
  int Y[] = { 4, 2, 3, 0, 9, 3, 5, 7 }; // definir vetor dados
  imprimir(Y, 8);
  ordInsercao(Y, 8);
  imprimir(Y, 8);
  }
   

# Ordena Insercao Direta
from __future__ import print_function; # imprime sem mudar linha Python 2
def imprimir (X, n) :
  print("(", end="");
  for i in range(n) :
    print("%3d " % X[i], end="");
  printf(")");

def ordInsercao (V, n) :
  for i in range(1, n) :
    aux = V[i]; # "abrir espaco" copiando V[i]
    j = i-1;
    while (j > -1 and V[j] > aux) : # "mova" para direita os maiores que aux
        V[j+1] = V[j]; # mover para direita V[j]
        j -= 1;
    V[j+1] = aux; # coloque aux na posicao correta

def main () :
  V = [4, 2, 3, 0, 9, 3, 5, 7]; # definir vetor dados 
  imprimir(V,8);
  ordInsercao(V, 8);
  imprimir(V,8);

main();

Bem, em resumo é isso. Experimente copiar esses códigos, tente algumas modificações, teste até estar seguro de ter compreendido.

Leônidas de Oliveira Brandão
http://line.ime.usp.br

Alterações:
2020/08/20: acerto no formato
2020/08/15: novo formato, pequenas revisões
2020/08/12: novo formato, pequenas revisões
2020/06/14: inserção de rótulos para as figuras
2019/06/16: versão inicial