O que é uma função em linguagens de programação
A ideia básica de uma função, implementada em alguma linguagem de programação, é encapsular um código que poderá ser invocado/chamado por qualquer outro trecho do programa. Seu significado e uso é muito parecido com o de funções matemáticas, ou seja, existe um nome, uma definição e posterior invocação à função.
Explicitando o paralelo com a matemática, tomemos como exemplo a função trigométrica cosseno(x):
deve-se definir a função (declará-la, seguindo a sintaxe correta: definir cosseno (parametro_real x): ...devolve valor;),
depois pode-se invocá-la com parâmetros efetivos, valores específicos, como: cosseno(0) ou cosseno(0.5).
Para quem deseja saber mais: Esta é uma função que é impossível de ser implementada de modo exato em um
computador digital, entretanto é viável obter boas aproximações utilizando o conceito de
série de Taylor.
Do ponto de vista prático, a série que aproxima a função cosseno, para valores de x próximo à origem é:
(1) cos(x) = 1 - x2 /2! + x4 /4! - x6 /6! + x8 /8! + ...
Note que o lado direito da equação (1) é a definição da função e ela está escrita em termos do parâmetro formal x. Ao "chamarmos" a função com parâmetros efetivos, é sobre o valor desses parâmetros que computamos o lado direito da expressão, por exemplo, computar cos(0.1) ou de cos(1.1).
Por que usar o conceito de função?
Assim, implementar códigos com objetivos específicos (como computar o cosseno de qualquer valor) apresentam três grandes vantagens:
- Facilita o desenvolvimento (desenvolvimento modular): implementa-se uma particular unidade, um trecho menor, concentrando-se nele, até que ele esteja funcionando com alto grau de confiabilidade;
- Organização: o código fica melhor organizado e portanto mais fácil de manter;
- Reaproveitamento: sempre que precisar aplicar o código encapsulado em qualquer outro trecho de código (ou noutro código), pode-se utilizar aquele que já foi implementado e é confiável.
Um exemplo de aplicação do conceito de função: conseguir deduzir algitmos complexos
Uma aplicação interessante das 3 vantagens acima citadas é possibilitar quebrar o problema, tentar perceber alguma estrutura
do problema que permita quebrá-lo em tarefas menores (e mais simples!).
Eesta abordagem é conhecida em Matemática como a técnica dividir para conquistar.
Em atividades mais sofisticadas (geralmente aquelas envolvendo laços "duplos" ou mais - i.e., "laço dentro de laço")
esta abordagem pode fazer a diferença entre conseguir deduzir um solução ou não conseguir.
Um exemplo básico da abordagem: deduzir um algoritmo para ordenar um vetor com N valores.
- Podemos imaginar um laço percorrendo as N posições do vetor V[], sequencialmente desde
V[0] até V[N-2]:
- Para cada posição i supor existir uma função que encontra e devolve o índice ind_min do menor valor entre V[i] e V[N-1];
- Como isso foi feito sucessivamente desde a posição i=0, então (por indução), temos neste momento:
V[0]<V[1]< ... V[i-1]< V[ind_min]< e
V[ind_min]<V[k] para todo k=i, i+1, ..., N-1 (supondo que a função acima funcionou).
Portanto, basta trocar o elemento atual da posição i com aquele da posição ind_min (que tem o menor dentre V[i], V[i+1], ..., V[N-1].
Deste modo estendemos a ordenação: V[0]<V[1]< ... V[i-1]< V[i]<.
Note que, em termos práticos, o algoritmo da parte "a" pode ser implementado como função, mas também pode-se
implementá-lo diretamente no código (sem função, porém neste caso resultará em um código ficará "menos organizado").
Experimente!
Introdução ao uso de funções em C e em Python
Assim, agrupar trechos com objetivos específicos e implementá-los na forma de uma função que ajuda bastante o desenvolvimento e a organização dos códigos em programação.
Do ponto de vista prático, a estrutura básica de uma função em uma linguagem de programação está representada abaixo, com a declaração da função e sua lista de parâmetros formais, seguido de sua invocação (quando providenciamos os parâmetro efetivos).
| Declaração: |
[enventual tipo de retorno] nome_da_funcao (lista_parametros_formais) comando1 ... comandoN return EXP |
| Uso: | var = nome_da_funcao(lista_parametros_efetivos) |
Atenção ao return, este é um comando especial, se ele for alcançado (e.g., ele pode estar subordinado a um comando de seleção if) então a execução da função é interrompida, retornando-se ao ponto imediatamente após o ponto de chamada da função. No caso do comando ter uma expressão qualquer, como indicado no exemplo return EXP, o valor de EXP é devolvido ao ponto de chamada, neste caso a chamada deve estar dentro de uma expressão (lógica ou artimética de acordo com o tipo de EXP) ou ser o lado direito de uma atribuição. Este último é o caso ilustrado na figura 1.
A lista de parâmetros pode conter vários nomes de variáveis, geralmente, separadas por vírgula. Por exemplo, se houver necessidade de uma função que realiza vários cálculos com três variáveis pode-se usar como declaração da função algo como: nome_da_funcao (var1, var2, var3).
Parâmetros formais e efetivos
De modo geral, a diferença entre os parâmetros formais e efetivos é que o primeiro corresponde ao nome da variável utilizada dentro da função, enquanto o segundo é o nome da variável que será usado para iniciar o parâmetro formal ao iniciar a execução da função.
Assim durante a execução, ao encontrar uma chamada à função nome_da_funcao, o fluxo de execução segue a partir do código da função. Mas antes de executar a primeira linha de código da função, os valores dos parâmetros efetivos servem para inicializar os parâmetros formais (que são também variáveis locais à função). Após esta inicialização, inicia-se a execução do código da função e geralmente ao final, encontra-se um comando do tipo "retorne devolvendo um valor" (return).
Ilustrando a execução de um trecho de programa com 3 chamadas à mesma função
Suponhamos que precisemos computar o valor da combinação de N tomado k a k, ou seja, C(N,k) = N! / ( k! (N-k)!). Para isso percebe-se que é necessário implementar o cômputo de fatorial que será utilizado 3 vezes. Para facilitar a compreensão, podemos escrever um código com 3 variáveis auxiliares para armazenar, respectivamente, N!, k! e (N-k)!.
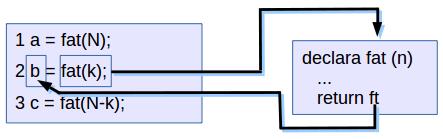
Fig. 1. Ilustração do fluxo de execução ao invocar uma função para computar o fatorial de um natural.
Na figura acima ilustra a execução do código para computar C(N,k), com o retângulo à esquerda contendo
o código que invoca a função fat e à direita a função fat.
Para entender o fluxo de execução destaremos a execução da linha 2, b = fat(k);.
Como b = fat(k); é uma atribuição, primeiro computa-se o valor do lado direito da atribuição
e só depois atribui-se à variável do lado esquerdo da atribuição o seu valor, ou seja,
1. primeiro executa-se o cômputo de fat(k), para isso
2. pega-se o valor do parâmetro efetivo k e usa-o para iniciar o parâmetro formal n da função
3. então inicia-se a execução da função fat
4. ao final da função fat, pega-se o valor da variável local ft e
5. atribui-se este valor para a variável b
6. então segue-se execução da próxima linha (3).
Vale notar que a execução da atribuição c = fat(N-k); seguirá um fluxo análogo aos 6 passos acima.
Uma vez entendido como é executado uma chamada á função, podemos novamente comparar com o conceito usual de função matemática. Existe a declaração da função, com seu parâmetro formal
fat : IN -> IN (nome 'fat', com domínio e imagem nos naturais)
fat(n) = { 1, se n=0, n x fat(n-1), se n>0 }
E existe o uso da função, como em
C(N,k) = fat(N) / (fat(k) x fat(N-k)
Exemplo concreto em C e em Python
Para ilustrar o uso e sintaxe de funções em C e em Python, examinemos um exemplo em que implementamos uma função para cômputo do fatorial de um natural n, que será o nome de seu único parâmetro formal.
| C | Python | ||||
|
|
|
Variáveis locais
Note na linha 2 do código acima que são declaradas duas novas variáveis, ft e i, dentro da fução fat. Isso significa que as variáveis ft e i são variáveis locais à função, ou seja, pode-se utilizar variáveis com os mesmos nomes em outras funções sendo que elas não terão qualquer relação. Em particular, na 11 do código em C ou na 9 do código em Python, poderia-se usar uma variável com nome n, ft ou i e ainda assim, está variável não teria qualquer relação com as correspondentes da função fat.
Para que serve função?
A partir do exemplo acima, para cômputo de C(n,k) = n! / (k! (n-k)!), imagine como seria o código para computar a combinção se a linguagem de programação NÂO dispusesse do conceito de funções: em resumo, precisariamos repetir as linhas 2 a 5 (ou 6), que computam fatorial, três vezes. Portanto, o uso de função simplifica o código.
Mas existe uma outra razão para usar funções, que não tão óbvia, a maior facilidade para escrever um programa. E isso se deve à vários fatores, mas principalmente à quebra de um problema maior em vários menores. Isso facilita o desenvolvimento e reduz a incidência de erros de programação.
Por exemplo, pode-se implementar a função separadamente, testando-a até que ela fique pronta e sem erros. Assim, o código fica mais fácil de ser entendido, pois ao usar a função pode-se abstrair, o trecho fica curto (apenas a chamada à função) e pode-se concentrar em saber se o restante do código está correto.
Leônidas de Oliveira Brandão
http://line.ime.usp.br
Alterações:
2020/08/15: novo formato, pequenas revisões
2020/08/09: Sábado, 09 de Agosto 2020, 14:00
2020/04/13: Segunda, 13 Abril 2020, 12:30