Introdução à eficiência de algoritmos

Nesta seção examinaremos uma questão essencial à computação, se o algoritmo é ou não eficiente para resolver o problema de interesse. Sobre isso existem vários aspectos que podem ser considerados, aqui examinaremos dois: a precisão e a velocidade.

Fig. 1. Representação de que maior velocidade de execução geralmente implica em menor precisão numérica.

A precisão diz respeito à "qualidade" da resposta, é necessário que ela seja suficientemente próxima da real solução para o problema considerado. Para ilustrar podemos considerar um exemplo numérico, por exemplo, tentar encontrar a raíz para determinada função f(.), ou seja, encontrar (se existir) algum x para o qual f(x)=0. Nesse caso, se o interesse estiver em pontos dentro do intervalo [0, 1], seria inútil se o ponto devolvido tivesse um erro maior que 0,5 (i.e., |f(x)| > 0,5).
Outro exemplo numérico é computar uma função transcendente como o cosseno de valor real. Uma vez as operações que um computador digita consegue efetivamente realizar são aquelas diretamente derivadas da soma, é preciso encontrar um algoritmo que compute uma boa aproximação para o cosseno(x), qualquer que seja o valor real x. Neste texto examinaremos as implementações para as funções seno e cosseno empregando o conceito matemático série de Taylor.

Quanto à velocidade, ela diz respeito ao tempo que o algoritmo leva para computar a resposta. É preciso que o tempo seja viável para o contexto, quer dizer que ao obter a resposta, essa ainda seja útil. Para ilustrar podemos considerar novamente o exemplo numérico da determinação da raíz da função f(.) (se existir, encontrar algum x para o qual f(x)=0). Digamos que o interessado seja uma industria de produção de tintas e que a raíz representa o melhor momento para interromper a produção de cada um de seus 300 pigmentos distintos. Nesse caso, se a resposta para cada função/pigmento demorar cerca de 10 minutos, então o método empregado é inviável, pois seria necessário cerca de 50 horas para obter as 300 raízes (50 x 10 min = 3000 min).
Um exemplo de outra natureza seria o contexto de planejamentos de pousos e aterrissagens em um grande aeroporto, após a ocorrência de algum evento não esperado, deve-se gerar uma nova escala para as próxima aterrissagens e decolagens muito rapidamente, antes que acabe o combustível de alguma aeronave em sobrevoo.

Como discutido no texto sobre ponto flutuante, o problema de precisão numérica inicia-se na impossibilidade de representar valores irracionais e mesmo dizimas periódicas que precisam ser truncados. Mas existe outra questão de eficiência, que é a precisão numérica do algoritmo utilizado para o cômputo. Um exemplo ilustrativo é acumular valores que crescem muito rapidamente (como funções exponenciais ou fatoriais) ou dividir por valores que aproximam-se de zero, ambos podem produzir resultados "ruins": estouro (ou transbordamento).

Como citado acima, um problema computacional é conseguir implementar funções que não podem ser escritas a partir de operações elementares de soma e multiplicação, com é o caso da função cosseno (que por isso é transcendental). Hoje, este não parece ser um problema, pois qualquer computador de bolso tem uma calculadora implementada que é capaz de computar boas aproximações para a função cosseno. Entretanto, isso só é possível por implementarem algum algoritmo eficiente, a partir de somas e multiplicações. No caso das funções trigonométicas, isso é feito usando a técnica matemática da série de Taylor. Isso será ilustrado nas tabelas 1 (implementação ineficiente) e 2 (implementação eficiente).

Existem problemas que sabidamente são intratáveis no sentido de sabermos, matematicamente, que é impossível existir um algoritmo que consegue resolvê-lo (como o problema da parada: não existe algoritmo que possa decidir se um algoritmo qualquer pára ou após um tempo finito de execução).

Existem outros tipos de problemas que supomos não ser possível resolvê-los eficientemente, ou seja, todas suas soluções conhecidas são ineficientes (tempo proporcional à uma função exponencial, de base maior que a unidade). Um exemplo nessa categoria, que denominada NP-Completo, é o problema da satisfatibilidade: encontrar valores para cada uma de suas variáveis, que são booleanas, de modo a tornar a expressão lógica verdadeira, como em f(b₁, b₂, b₃) = b₁ E (b₂ OU não b₃). Para esse caso, por ser uma instância pequena do problema, é fácil perceber que a resposta é sim, basta tomar b₁ e b₂ como verdadeiro (não importando o valor de b₃ pode ser verdadeiro ou falso). A solução conhecida para a satisfatibilidade é tentar todas as 2ⁿ possibilidades para as n variáveis! Se o n for grande, é inviável esperar por uma resposta. Exemplo para n=3: testar com     f(verdadeiro,verdadeiro,verdadeiro), f(verdadeiro,verdadeiro,falso),     f(verdadeiro,falso, verdadeiro), f(verdadeiro,falso, falso),     f(falso, verdadeiro,verdadeiro), f(falso, verdadeiro,falso),     f(falso, falso, verdadeiro), f(falso, falso, falso).

Na seção seguinte examinaremos um particular problema, conseguir um valor aproximado para a função trigonométrica cosseno, explorando tanto a questão da eficiência numérica (precisão) quanto a de tempo de execução (velocidade).

A função cosseno, assim como várias outras, não pode ser computada de modo exato em um computador digital, em razão de ser uma função transcendente (basicamente, significa que não pode ser computada a partir de somas). Então usamos uma teoria matemática apresentada em 1715, aproximá-la por uma função polinomial que tem como propriedade ter todas as derivadas coincidindo com as derivadas da função a ser aproximada, considerando determinado ponto fixado. Esse polinômio de infinitos termos, recebeu o nome de série de Taylor, devido seu proponente Brook Taylor.

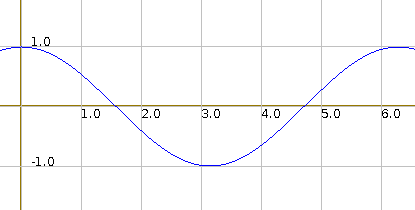Como a função cosseno é periódica, de período 2*Π e além disso os valores em cada quadrante coincidem em módulo, podemos computar apenas para primeiro caso, para x entre 0 e Π/2. Desse modo, podemos usar um caso particular da série de Taylor, a séria aplicada ao ponto x=0, que neste caso é chamada de série de MacLaurin. Fixado um valor real x entre 0 e Π/2, a série de MacLaurin que aproxima o cosseno aplicado ao ponto x=0, cos(x), é o polinômio (de infinitos termos) p(x)=a₀+a₁x¹+a₂x²+a₃x³+... de tal forma que a k-ésima derivada de p(0) coincide com a k-ésima derivada de cos(0), ou seja, cos(0)=p(0), cos'(0)=p'(0), cos''(0)=p''(0) e assim por diante.

Assim, no caso da função cosseno, escrevendo o polinômio candidato p(x) = a₀ x⁰ + a₁ x¹ + a₂ x² +... e estabelecendo as identidades para cada derivada e usando x=0 e sabendo que cos(0)=1, sen(0)=0, que cos'(x)=-sen(x) e que sen'(x)=cos(x)=, obtém-se
    p(0)=a₀ ⇒ a₀ = 1
    p'(0)=a₁+2a₂x¹+3a₃x²+...|x=0 ⇒ p'(0)=a₁ ⇒ a₁ = p'(0)= -sen(0) = 0 ⇒ a₁ = 0
    p''(0)=2a₂+6a₃x¹+12a₄x²+...|x=0 ⇒ (1/2)p''(0)=a₂ ⇒ a₂ = (1/2)(-cos(0)) = -1 ⇒ a₂ = -1/2
    p'''(0)=6a₃+24a₄x¹+...|x=0 ⇒ (1/6)p'''(0)=a₃ ⇒ a₃ = (1/6)(cos'''(0)) = (1/3!)(-sen''(0)) = (1/3!)(-cos'(0)) = (1/3!)sen(0) = (1/3!)0 ⇒ a₃ = 0
e assim, por diante, obtendo-se o polinômio aproximador:
        cos(x) = 1 - x² /2! + x⁴ /4! - x⁶ /6! + x⁸ /8! + ...

i = 0;
while (i<2*NT) { // Ineficiente! Nao implemente assim!
     soma = soma + pot(-1, 2*i) * pot(x, 2*i) / fat(2*i);
     i += 2;
     }

i = 0;
while (i<2*NT) : # Ineficiente! Nao implemente assim!
     soma = soma + pot(-1, 2*i) * pot(x, 2*i) / fat(2*i);
     i += 2;
     
  return soma;

float cossInef (float x) {
  float pot = 1, soma = 0;
  float termo0 = 2, termo = 1;
  int fat = 1, i = 1, sinal = 1;
  while (valor_absoluto(termo0-termo)>Lim) {
     soma = soma + termo;
     pot *= x * x; // compute potencia 2i de x
     fat *= (i+1) * (i+2); // compute fatorial de 2i
     termo0 = termo;
     termo = sinal * pot / fat;
     i += 2;
     sinal = -sinal;
     }
  return soma;
  }

def cossInef (x) :
  pot = 1; soma = 0;
  termo0 = 2; termo = 1;
  fat = 1; i = 0; sinal = 1;
  while (valor_absoluto(termo0-termo)>Lim) :
     soma = soma + termo;
     pot *= x * x; # compute potencia 2i de x
     fat *= (i+1) * (i+2); # compute fatorial de 2i
     termo0 = termo;
     termo = sinal * pot / fat;
     i += 2;
     sinal = -sinal;
  return soma;

// Leo^nidas O. Brandao - 2017/06/19
// cos(x) = 0! x^0 - x^2 /2! + x^4 /4! - x^6 /6! + x^8 /8! + ...
//        = 1 - x^2 /2! + x^4 /4! - x^6 /6! + x^8 /8! + ...
// gcc -lm -o introducao_eficiencia_algoritmos_cosseno introducao_eficiencia_algoritmos_cosseno.c

#include <stdio.h>
#include <math.h> // cos(x)
#include <time.h> // clock_t, clock()

#define Lim 0.001

float valor_absoluto (float x) {
  if (x>=0) return x;
  return -x;
  }

// Cosseno implementado de modo ineficiente
float cossInef (float x) { ... } // copiar aqui o codigo C do ineficiente acima

// Cosseno implementado de modo mais eficiente
float cossEfic (float x) {
  float pot = 1, soma = 0;
  float termo0 = 2, termo = 1;
  int i = 0, sinal = 1;
  while (valor_absoluto(termo0-termo)>Lim) {
     soma = soma + termo;
     termo0 = termo;
     termo *= -1 * x * x / ((i+1) * (i+2)); // compute potencia 2i de x e fatorial de 2i
     i += 2;
     }
  return soma;
  }

int main (void) {
  float x, cosx, auxcI, auxcE;
  int i;
  clock_t tempo_inicial = clock(); // "dispara o cronometro"...
  printf("    x | ineficiente | eficiente | math cos(x) | dist inef. | dist efic.\n");
  x = 0.0;
  for (i=0; i<10; i++) {
    cosx = cos(x);
    auxcI = cossInef(x);
    auxcE = cossEfic(x);
    printf(" %3.2f | %11.4f | %9.4f | %11.4f | %10.4f | %10.4f\n",
           x, auxcI, auxcE, cosx, valor_absoluto(auxcI-cosx), valor_absoluto(auxcE-cosx));
    x += 0.05;
    }
  clock_t tempo_final = clock();
  printf("Tempo em segundos: %f\n", (double)(tempo_final - tempo_inicial) / CLOCKS_PER_SEC);

  return 1;
  }

# Leo^nidas O. Brandao - 2017/06/19
# cos(x) = 0! x^0 - x^2 /2! + x^4 /4! - x^6 /6! + x^8 /8! + ...
#        = 1 - x^2 /2! + x^4 /4! - x^6 /6! + x^8 /8! + ...

# Invocar execucao com linha de comando: python introducao_eficiencia_algoritmos_cosseno.py

import math; # para cos(x)
import time; # para tempo 'time.time()'

Lim = 0.001

def valor_absoluto (x) :
  if (x>=0) : return x;
  return -x;

# Cosseno implementado de modo mais eficiente
def cossInef (x) : # Copiar aqui a implementacao de cosseno ineficiente
  ...
		
# Cosseno implementado de modo mais eficiente
def cossEfic (x) :
  pot = 1; soma = 0;
  termo0 = 2; termo = 1;
  i = 0; sinal = 1;
  while (valor_absoluto(termo0-termo)>Lim) :
     soma = soma + termo;
     termo0 = termo;
     termo *= -1 * x * x / ((i+1) * (i+2)); # compute potencia 2i de x e fatorial de 2i
     i += 2;
  return soma;

def main () :
  tempo_inicial = time.time(); # "dispara o cronometro"...
  print("    x | ineficiente | eficiente | math cos(x) | dist inef. | dist efic.");
  x = 0.0;
  for i in range(0, 10) :
    cosx = math.cos(x);
    auxcI = cossInef(x);
    auxcE = cossEfic(x);
    print(" %3.2f | %11.4f | %9.4f | %11.4f | %10.4f | %10.4f" %
         ( x, auxcI, auxcE, cosx, valor_absoluto(auxcI-cosx), valor_absoluto(auxcE-cosx) ));
    x += 0.05;

  tempo_final = time.time();
  print("Tempo em segundos: %f\n" % (tempo_final - tempo_inicial));

main();

    x | ineficiente | eficiente | math cos(x) | dist inef. | dist efic.
 0.00 |      1.0000 |    1.0000 |      1.0000 |     0.0000 |     0.0000
 0.05 |      1.0012 |    0.9988 |      0.9988 |     0.0025 |     0.0000
 0.10 |      1.0050 |    0.9950 |      0.9950 |     0.0100 |     0.0000
 0.15 |      1.0112 |    0.9888 |      0.9888 |     0.0225 |     0.0000
 0.20 |      1.0199 |    0.9801 |      0.9801 |     0.0399 |     0.0000
 0.25 |      1.0311 |    0.9689 |      0.9689 |     0.0622 |     0.0000
 0.30 |      1.0447 |    0.9553 |      0.9553 |     0.0893 |     0.0000
 0.35 |      1.0606 |    0.9394 |      0.9394 |     0.1213 |     0.0000
 0.40 |      1.0789 |    0.9211 |      0.9211 |     0.1579 |     0.0000
 0.45 |      1.0996 |    0.9004 |      0.9004 |     0.1991 |     0.0000

                   C          Python      
Tempo em segundos: 0.000079   0.000220

              C          Python
Tempo medio:  0.000520   0.008276
Tempo minimo: 0.000016   0.000076
Tempo maximo: 0.000945   0.016031