Para explicar as razões pelas quais deve-se evitar comandos de entrada e de saída dentro da definição de uma função, devemos primeiro enfatizar o que é a uma função em linguagens como C ou Python:

• é um código que recebe seus dados de entrada a partir de uma lista de parâmetros (parâmetros formais);
• é um código que processa os dados de entrada e geralmente devolve algum valor como resposta (em seu comando return);
• é um código que pode ser invocado a partir de outros trechos do programa, que providenciam os valores para os parâmetros (parâmetros efetivos).

Desse modo, usando como exemplo a função fatorial (fat(0)=1 e fat(n)=n*fat(n-1), n>0), a razão para se evitar comandos de entrada e de saída dentro da definição da função pode ser resumida em:

• Facilita o reúso de código, ou seja, sempre que precisar de um algoritmo que compute o fatorial, basta copiar o código que já implementou (e testou);
• Facilita o desenvolvimento de programas maiores, pois pode-se agrupar os blocos lógicos que tenham um propósito bem definido como uma função.

A fim de ficar mais clara a vantagem de passar os valores via parâmetro, pense na implementação errônea da função fat, suponha que em seu código tenha sido usado um comando para leitura (via teclado) dos dados. Então, se precisar computar a combinação de n, tomados k a k (C_n,k=n!/((n-k)!k!)), esse valor não poderá ser computado usando a expressão seguinte (com chamada à função fat): fat(n)/(fat(n-k)fat(k)).
Por que mesmo? Porque, os valores a partir dos quais desejamos saber a combinação já são dados, não faz sentido obrigar o usuário a digitar os valores de n, de n-k e de k (além disso ele pode digitar errado!).

Assim, nos exercícios que apresentam o conceito de função (portanto envolvendo um bloco lógico com propósito bem definido), exigiremos que o aprendiz não use comandos de entrada ou de saída de dados dentro da função. Com isso esperamos que ele adquira bons hábitos de programação.

Entretanto, existem as exceções, exemplos nos quais é útil usar comando de entrada ou de saída dentro da função. Ilustraremos o caso de utilidade de um comando de saída dentro da função, isso ocorre se desejamos computar (e imprimir) os n primeiros termos da sequência de Fibonacci. Então, naturalmente precisaremos do comando de impressão/saída e como isso pode ser feito para qualquer n é adequado agrupar esse código na forma de um procedimento separado (no caso uma função sem valor de retorno).
Porém se o objetivo fosse conhecer apenas o termo n da sequência, a função não deveria ter o comando de saída.

Uma última observação sobre os exercícios envolvendo funções. O programa principal sempre deve ter ao menos um comando para entrada e ao menos um para saída de dados. Sem eles não seria possível testar se a função do exercício foi implementada corretamente ou não.

Suponha que precisemos fazer um program para computar quantas são as combinações de n termos combinados k-a-k, ou seja, tendo n elementos, desejamos saber de quantos modos distintos podemos formar grupos com k dos elementos.

Esse conceito aparece em probabilidade e em combinatória, sabemos que esta combinação corresponde ao agrupamentos de elementos nos quais a ordem não importa (tanto faz a ordem dos k elementos do tipo a) e que a fórmula que fornece o total desses subconjuntos é a seguinte:

Por exemplo, combinar 6 valores distintos, tomados 2 a 2 resulta 15=6!/((6-2)!2!)=6!/(4!2!), que são os 15 subconjuntos: (6,5), (6,4), (6,3), (6,2), (6,1), (5,4), (5,3), (5,2), (5,1), (4,3), (4,2), (4,1), (3,2), (3,1), (2,1).

Assim, existem duas possibilidades de implementar esse código, uma implementando a função fatorial (fat(n)) que seria invocada três vezes pelo programa principal (com algo como imprima(fat(n) / (fat(k) * fat(n-k)). Outra possibilidade é implementar também o cômputo de fat(n) / (fat(k) * fat(n-k)) também como uma função. Apesar dessa segunda possibilidade não ajudar tanto na organização do código (pois a segunda função (comb(n,k)) seria muito simples, ilustraremos dessa forma por ela usar função chamando função que chama função (a principal chama comb(n,k) e essa chama fat(n)). Veja como ficaria o código em uma pseudo-linguagem de programação:

int fat(n) { //# estou supondo que o valor digitado pelo usuario seja um natural maior ou igual a 0 (n>=0)
  valfat = 1;
  cont = 2;
  enquanto (cont<=n) { //# continue computando enquanto nao chegar ao valor cont==n
    valfat = valfat * cont;
    cont = cont + 1;	    
    }
  devolva valfat;
  }
int comb(n, k) {
  devolva fat(n) / (fat(n-k)*fat(k));
  }
principal() {
  declara_inteiros N, k; //# note que os nomes de variaveis daqui tem relacao NULA com os usados em 'fat'
  declara_inteiros a, b, c; //# para uma segunda versao
  leia(N, k); //# leia 2 valores naturais e armazene-os respectivamente em N e em k (espera-se que digite N>=k)
  //# pode-se invocar seguidamente fat 3 vezes como abaixo:
  imprima(comb(N,k);
  //# pode-se invocar a funcao fat 3 vezes e armazenar cada resultado e depois "imprimir"
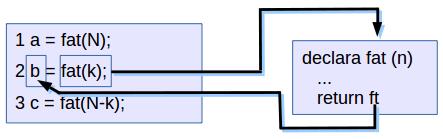
  a = fat(N);
  b = fat(k);
  c = fat(N-k);
  imprima(a/( b * c))); //# este exemplo e' ilustrado na figura abaixo
  }

Novamente para enfatizar as desvantagens de usar leitura ou impressão dentro de funções, procure implementar o código acima, em sua linguagem favorita, e colocar nele comandos para leitura ou saída dentro da função fat(n), como discutido abaixo.

Note que se dentro da função fat houvesse um comando do tipo leia(n); a função NÃO poderia ser usada, pois ao ser invocada as 3 vezes, em cada uma delas exigiria que o usuário digitasse novamente o valor para N inicialmente (estragando o valor de N passado para a função), depois exigiria a digitação novamente do k e por último haveria o absurdo de exigir que o usuário digitasse o valor para N-k.

De forma análoga, se a função fat tivesse algum comando de saída, ao usar a função 3 vezes, o usuário receberia informações confusas: ele deseja a combinação de n combinados k-a-k, mas receberia 4 infomações (n!, k!, (n-k)! e n!/(k! (n-k)!))))).

Se rodarmos este programa seguidamente, na ordem das colunas (primeiro a única entrada de Entradas 0, depois a primeira linha de Entradas 1, depois sua segunda linha e assim por diante até a última linha de Entradas 4) e agruparmos as saídas de cada coluna em uma única linha, obteremos a tabela na última coluna abaixo (Saídas (cada linha um dos blocos de entradas)). Destacamos três dos valores para mostrar a relação do Triângulo de Pascal

   0
   1
   2
   3
   4

 1   0

 1   1
 1   0

 2   0
 2   1
 2   2

 3   0
 3   1
 3   2
 3   3

 4   0
 4   1
 4   2
 4   3
 4   4

 1
 1   1
 1   2   1
[1] [3]   3   1
 1  [4]   6   4   1

Examinando as saídas (ũltima coluna) notamos uma propriedade interessante: o elemento da linha n+1, coluna k+1 = o elemento da linha n, coluna k + o elemento da linha n, coluna k+1. Veja por exemplo, a última linha, linha 4: o segundo elemento = 4 = 1 + 3 (da linha acima).

Leônidas de Oliveira Brandão
http://line.ime.usp.br