Introdução à recorrência/recursividade em algoritmos

Nesta seção examinaremos o conceito de algoritmos recorrentes, ou recursivos. A ideia de recursividade é a de um processo que é definido a partir de si próprio. No caso de um algoritmo, esse é definido invocando a si mesmo.
Outros materiais sobre recursividade: fatorial recursivo e busca binária; sobre gerao de números binários.

Exemplos de imagens envolvendo recursividade são os fractais geométricos, como no fractal que apelidamos de Tetra-Círculo, formado por circunferências com metade do raio original, construídas a partir dos pontos médios entre seus polos e seu centro, como na imagem abaixo.

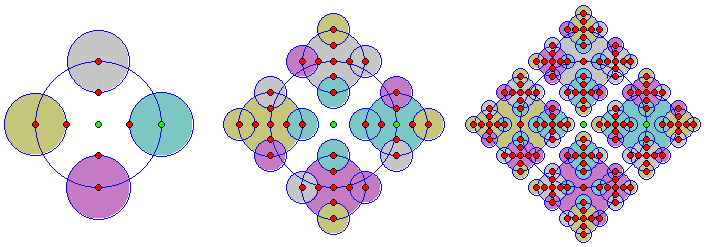
Fig. 1. Representações dos 3 primeiros níveis de recorrência para construir o fractal tetra-círculo.

Após estudarem o material dessa página, examinem essa página que tem mais exemplos de algoritmos recursivos.

Na área da computação, existe um importante projeto cujo nome é uma brincadeira envolvendo recursividade, o projeto GNU. Uma das página do projeto, na qual é explicado o significado do acrônimo GNU, encontramos: The name 'GNU' is a recursive acronym for "GNU's Not Unix". Que em uma tradução direta poderia ser: GNU não é Unix,

Um outro exemplo de recursividade pode ser obtido ao conectar uma câmera à uma tela de computador, jogando a imagem capturada para a tela, usando como foco de captura a própria tela. Criamos a imagem a seguir dessa forma (usando software do projeto GNU).

Fig. 2. Filmando uma tela com o resultado da filmagem.

Vamos examinar dois exemplos simples funções recursivas, que apenas imprimem um contador. Mas ilustraremos o comportamento em uma delas fazendo um impressão antes e na outra após a volta da chamada recursiva.
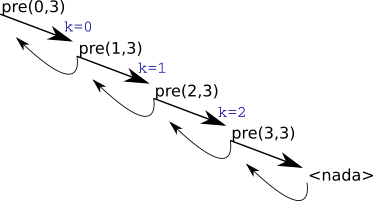
Simulando a função pre(n,k). Alguma outra função invoca inicialmente pre(0,3), ao entrar 0!=3 então executa print(" k=%d" % 0) e dai a chamada pre(0+1,3). Dentro de pre(1,3), como 1!=3, executa print(" k=%d" % 1) e dai invoca pre(1+1,3). Dentro de pre(2,3), como 2!=3, executa print(" k=%d" % 2) e dai invoca pre(2+1,3). Dentro de pre(3,3), como 3==3, executa return, voltando para a chamada pre(2,3), mas não existe mais comandos a partir do ponto de retorno, então volta para a chamada pre(1,3), na qual novamente não existe mais comandos, então volta para a chamada pre(0,3), na qual novamente não existe mais comandos, então volta para a função que primeiro chamou a função.

Exemplo de Funções recursivas com impressão antes e depois da chamada recursiva C Python #include <stdio.h> void pre (int k, int N) { if (k==N) return; printf(" k=%d\n", k); pre(k+1, N); } void pos (int k, int N) { if (k==N) return; pos(k+1, N); printf(" k=%d\n", k); } void main (void) { printf("pre:\n"); pre(0, 3); printf("pos:\n"); pos(0, 3); } def pre (k, N) : if (k==N) : return; print(" k=%d" % k); pre(k+1, N); def pos (k, N) : if (k==N) : return; pos(k+1, N); print(" k=%d" % k); def main () : print("pre:"); pre(0, 3); print("pos:"); pos(0, 3); main();

Fig. 3. As imagens ilustram as pilhas de execução para as funções pre(0,3) e pos(0,3).

Para entender um novo conceito é sempre interessante examiná-lo sob alguma perpectiva conhecida, assim talvez valha a pena pensar na definição (simplificada) recursiva do conceito de expressão aritmética (EA). O conceito de EA é introduzido ainda no ensino fundamental, mas de modo informal, a partir de exemplos, então como fazer para definir formalmente o conceito? Uma maneira de fazer isso é usar novamente uma definição recorrente, vejamos com fazer isso usando apenas operadores de soma e de subtração:

  EA := constante
  EA := EA + EA
  EA := EA * EA
  EA := (EA)
  EA := -EA

Ou seja, na regra 1 trata do caso básico, qualquer constante numérica, por definição é uma EA (isso define a "base da recorrência"). As demais regras definem recursivamente uma EA, por exemplo, se EA1 e EA2 são uma expressões aritméticas corretas, então também são expressões aritméticas corretas as composições "EA + EA", "EA * EA", "(EA)" e "-EA". Experimente o conceito com "2" e "2-3" no lugar de EA1 e EA2.

Entretanto, chamamos a atenção para essa definição ser uma simplificação, pois ela não elimina ambiguidades, e.g., para a expressão (sintaticamente correta) "2+3*2", existem dois possíveis resultados... Pois a sequência EA -> EA+EA -> 2+EA -> 2+EA*EA -> 2+EA*2 -> 2+3*2 -> 2+6 -> 8 resulta 8, mas EA -> EA*EA -> EA*2 -> EA+EA*2 -> 2+3*2 -> 5*2 -> 10 resulta 10. Para entender a ordem das substituições veja a imagem abaixo.

  
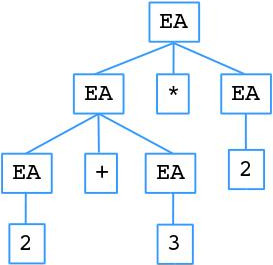
Fig. 4. A árvore da esquerda produz como resultado para a expressão o valor 8 e a da direita resulta 10.

Outro exemplo interessante é função fatorial, geralmente apresentada no Ensino Médio como n! = 1, sempre que n=0, caso contrário n! = n*(n-1)!. Ou seja, no caso geral, a definição da função usa ela própria, de modo recorrente, esse é o princípio de uma função recursiva/recorrente. Usando a notação usual de função matemática, a função fatorial pode ser definida como: f:D->I, sendo f(n) = { 1, se n=0; n*f(n-1), se n>0}.

Um primeiro exemplo de função matemática intrinsicamente recursiva é a função fatorial (digamos fat: IN -> IN). Geralmente no Ensino Médio essa função é apresentada de modo informal, a partir de exemplos: fat(0) = 1, fat(1) = 1, fat(2) = 2 e generaliza-se afirmando que fat(n) = n x (n-1) x (n-2) x ... x 2 x 1. E o sentido das reticências é inferido.

Mas pode-se apresentar uma definição foraml para fatorial dizendo-se que o fatorial de 0, é 1 e que o fatorial de n, para n > 0, é o produtudo de n pelo fatorial de n-1, ou seja,

Assim, como no lado direito da definição da função fatorial usa-se a própria função fatorial, essa é uma definição recursiva. Todas as funções recursivas tem essa característica, o nome da função aparecer tanto à esquerda, quanto à direita do símbolo de atribuição (=).

De modo prático, sem nos preocuparmos ainda com a implementação e execução de um algoritmo, para computar, por exemplo, fat(4) = 4 x fat(3) = 4 x 3 x fat(2) = 4 x 3 x 2 x fat(1) = 4 x 3 x 2 x 1 x fat(0) = 4 x 3 x 2 x 1 x 1 = 24. Para ver com mais detalhes como é realizada as chamadas recursivas na função fatorial, siga este apontador.

Geralmente as liguagens de programação permitem definições recursivas de funções. Comecemos examinando precisamente a função fatorial. Implementando-a de modo iterativo fazemos algo como fat = 1; for i de 2 até N : fat = fat * i;, ou seja, usamos uma variável contadora para enumerar os naturais entre 2 e N e interrompemos a repetição quanto i chegar a N.

No caso da definição recursiva de fatorial, o processo de chamada recursiva deve ser interrompido quanto n tiver o valor 0. Então essa condição deve aparece no início da definição da função (caso contrário, ocorrerá um laço infinito). Na tabela abaixo, apresentamos implementações recursivas para a função fatorial tanto na linguagem C, quanto em Python.

#include <stdio.h>
// Fatorial recursivo
int fatRec (int n) {
  if (n==0) return 1;     // final de recorrencia
  return n * fatRec(n-1); // senao devolve n x "o fatorial de n-1" (inducao)
  }

// experimente invocar esta versao com msg para rastrear execucao
int fatRecDepuracao (int n) {
  int aux;
  if (n==0) { printf("fat(%d)\n", n); return 1; }    // final de recorrencia
  aux = n * fatRecDepuracao(n-1); // senao devolve n x "o fatorial de n-1" (inducao)
  printf("fat(%d): devolve %d\n", n, aux);
  return aux;
  }

int main (void) {
  int n;
  scanf("%d", &n);
  printf("O fatorial de %d e': %d\n", n, fatRec(n));
  return 1;
  }

# Fatorial recursivo
def fatRec (n) : # os finalizadores ';' sao opcionais em Python
  if (n==0) : return 1;   # final de recorrencia
  return n * fatRec(n-1); # senao devolve n x "o fatorial de n-1" (inducao)

# experimente invocar esta versao com msg para rastrear execucao
def fatRecDepuracao (n) :
  if (n==0) : print("fat(%d)" % n); return 1; # final de recursao (final de "laco")
  aux = n * fatRecDepuracao(n-1);              # senao faca mais um "passo" (inducao)
  print("fat(%d): devolve %d\n", n, aux);
  return aux;

def main () :
  n = int(input());
  print("O fatorial de %d e': %d" % (n, fatRec(n)));

main();

Vamos usar o exemplo do fatorial para ilustrar como é possível que o computador execute funções recursivas. O truque computacional é mais ou menos o seguinte: ao fazer a chamada fat(n), em um contexto que denominaremos n,

1. inicia-se a execução do comando n x fat(n-1), mas fat(n-1) ainda não é conhecido, desse modo registra-se em uma "pilha" (empilhar) este ponto de execução; e
2. invoca-se novamente a função, dessa vez com fat(n-1) (contexto n-1);
3. quando o computador tiver finalmente o valor para fat(n-1), desempilha-se o contexto n (portanto, volta-se ao cômputo de n x fat(n-1), mas agora fat(n-1) é conhecido), realiza-se a produto e devolve o resultado.

Exemplificando esse processo na função fatRec com parâmetro efetivo com valor 4, ou seja, f(4), executa-se o comando 4 * fatRec(3) e, quando o computador tiver conseguido computar fatRec(3), esse valor (6) é substituido no contexto 4 (i.e., 4 * 6) e devolve-se o resultado desse produto (24).

Vamos detalhar um pouco mais esse processo de recorrência, mas agora usando fatRec(3). Na primeir coluna indicamos a ordem de execução de cada instrução (Ord.), na segunda o contexto n

Ord.  n  Imprimir (esquema de execução)
   1  3  fatRec(3)        
   2  2  = 3 * fatRec(2) --> fatRec(2)
   3  1                      = 2 * fatRec(1) --> fatRec(1)
   4  0                                          = 1 * fatRec(0) --> fatRec(0)
   5  0                                                              = 1 // final recorrencia, volta onde foi chamado
   6  1                                          = 1 * 1 = 1 // final recorrencia 'fatRec(1)', volta para quem chamou
   7  2                      = 2 * 1 = 2 // final recorrencia 'fatRec(2)', volta para quem chamou
   8  3  = 3 * 2 = 6 // final recorrencia 'fatRec(3)' e dai imprime o valor 6

Note que na ordem de cada instrução, separamos o comando k * fatRec(k-1) em duas instruções, primeiro obter o valor de fatRec(k-1), digamos FK, e depois a instrução k * FK.

Para um outro exemplo de implementação recursiva podemos usar o cômputo da progressão de razão 1, e.g. a soma dos naturais até n.

#include <stdio.h>
// P.A.
int somaRec (int n) {
  if (n==0) return 0;      // final de recorrencia
  return n + somaRec(n-1); // senao devolve n + soma ate n-1 (inducao)
  }

int main (void) {
  int n;
  scanf("%d", &n);
  printf("A soma dos naturais ate' %d e': %d\n", n, somaRec(n));
  return 1;
  }

# P.A.
def somaRec (n) :
  if (n==0) : return 0;    # final de recorrencia
  return n + somaRec(n-1); # senao devolve n + soma ate n-1 (inducao)

def main () :
  n = int(input());
  print("A soma dos naturais ate' %d e': %d" % n, somaRec(n));

main();

Note que não é necessário colocar a palavra reservada else após o if, pois a linha após o comando if só será executada se, e somente se, a condição da seleção resultar falso, ou seja, se o comando subordinado ao if NÃO for executado. Por que mesmo? (se não deduzir a razão, consulte a nota A ao final)

Experimente copiar os códigos para a função fatorial e para a enumeração dos primeiros naturais, eventualmente coloque mais mensagens para depuração (e.g. imprimir Entrei na funcao com n=%d e Chamei recursivamente com n-1=%d) e certifique-se que entendeu bem recorrência.

Um exemplo interessante para ilustrar o quanto alguns programas ficam mais simples se deduzidos na forma recursiva é desenhar um algoritmo para gerar todos os números binários com exatamente k bits (considerandos os "zeros à esquerda").

Decimal Binário | Decimal Binário 0 0000 | 8 1000 1 0001 | 9 1001 2 0010 | 10 1010 3 0011 | 11 1011 4 0100 | 12 1100 5 0101 | 13 1101 6 0110 | 14 1110 7 0111 | 15 1111

Fig. 5. Ilustração da sequência recursiva a ser seguida pelo algoritmo.

Exemplo: todos os binários com até 4 dígitos (com seu correspondente decimal à esquerda)

Antes de ler o texto explicando como resolver este problema, pense um pouco sobre ele. Primeiro, tente por alguns minutos esquematizar um algoritmo para resolver o problema de modo iterativo (não recursivo), depois tente resolvê-lo de modo recursivo. Se conseguir resolver o desafio, poderá pereceber o quanto a recorrência simplifica a resolução desse problema.

Entretanto, se você está com dificuldades para resolver o problema, siga este apontador para ver uma sugestão de como estruturar o pensamento para resolver o problema de forma recursiva.

Agora que você sabe como gerar todos os binários com até k dígitos, pense em generalizar a problema, ou seja, gerar todos os números, em qualquer base, com até k dígitos. Espero que perceba que essa generalização é bem simples para quem resolveu o caso com base 2 (binário).

As duas seções seguintes são conceitualmente mais sofisticadas, portanto mais difíceis de ser compreendidas por um aluno de um curso introdutório de programação, em particular, a próxima seção sobre as Torres de Hanói é mais difícil. Desse modo, estude-as apenas se estiver muito confortável com o conceito de recorrência.

Pode-se notar nos exemplos anteriores que um algoritmo recursivo (geralmente) é mais simples de ser codificado. Um exemplo que ilustra ainda melhor essa facilidade é implementar um algoritmo para simular (ou computar) os movimentos do problema das Torres de Hanói.

Neste problema o objetivo é mover n discos da haste A para a haste C, seguindo as regras do "jogo" (e.g., nunca um disco maior pode ficar sobre um de diâmetro menor). Assim, para mover os n pode-se supor que exista um algoritmo que consiga realizar a movimentação mínima de n-1 discos (indução) e invocá-lo para retirar todos os n-1 discos que estão sobre si, movendo-os para a haste auxiliar B. Isso libera também a haste C e pode-se mover o maior disco de A para C, com o menor nũmero possível de moviemtos: apenas 1. Então, pode-se novamente invocar o algoritmo para mover otimamente os n-1 que estão na haste B para a haste C, resolvendo o problema.

A ideia acima está representada nas figuras abaixo e dela percebe-se claramente um algoritmo recursivo para resolver o problema.

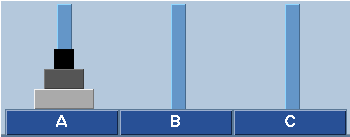
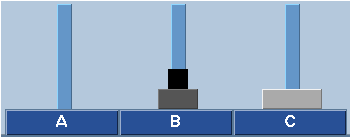
Fig. 6. Ilustração da sequência de movimentação mínima para 3 discos.

moverHanoi(n, A, C, B) - mover n discos de A para C, usando a haste B
  se n==1, entao mover disco do topo da haste A para a haste C - final de recorrencia
  senao
    moverHanoi(n-1, A, B, C) - mover otimamente n-1 discos de A para C (libera o ultimo)
    mover disco do topo da haste A para a haste C
    moverHanoi(n-1, B, C, A) - mover otimamente n-1 discos de B para C

Entretanto, a recursividade pode não ser eficiente! O melhor exemplo de ineficiência é tentar implementar um algoritmo recursivo para gerar a sequência de Fibonacci: 1, 1, 2, 3, 5, 8, 13, ... ou seja, matemamticamente podemos definir a função de Fibonacci F_n = 1, se n=1 ou n=2, senão F_n = F_n-1 + F_n-2, para todo n>2.

Uma implementação iterativa eficiente para gerar o n-ésimo termo da sequência de Fibonacci pode ser: F1=1; F2=1; for i de 3 até N : F = F1+F2; F1=F2; F2=F;

Novamente a implementação recursiva tem um código mais "enxuto", porém exponencialmente ineficiente! Isso está ilustrado no código abaixo que implementa ambos e compara o tempo de execução tanto em C quanto em Python.

#include <stdio.h>
#include <time.h> // clock_t, clock()

// Fibonacci iterado
int fib (n) { // os finalizadores ';' sao opcionais em Python
  int i, F1=1, F2=1, F;
  if (n<3) return 1;
  for (i=3; i<=n; i++) {
    F = F1+F2;
    F1 = F2;
    F2 = F;
    }
  return F;
  }

// Fibonacci recursivo
int fibRec (n) { // os finalizadores ';' sao opcionais em Python
  if (n==1 || n==2) return 1;       // final de recorrencia
  return fibRec(n-1) + fibRec(n-2); // senao devolve
  }

int main (void) {
  int n, fibA; clock_t tempo_inicial, tempo_final;
  scanf("%d", &n);

  tempo_inicial = clock(); // "dispara o cronometro"...
  fibA = fib(n);
  tempo_final = clock();
  printf("Iterativo: %3d - %3d em %f segundos\n",
         n, fibA, (double)(tempo_final - tempo_inicial) / CLOCKS_PER_SEC);

  tempo_inicial = clock(); // "dispara o cronometro"...
  fibA = fibRec(n);
  tempo_final = clock();
  printf("Recursivo: %3d - %3d em %f segundos\n",
         n, fibA, (double)(tempo_final - tempo_inicial) / CLOCKS_PER_SEC);
  return 1;
  }

import time; # para tempo 'time.time()'

# Fibonacci iterado
def fib (n) : # os finalizadores ';' sao opcionais em Python
  F1=1; F2=1;
  if (n<3) : return 1;
  for i in range(3, n+1) :
    F = F1+F2;
    F1 = F2;
    F2 = F;
  return F;

# Fibonacci recursivo
def fibRec (n) : # os finalizadores ';' sao opcionais em Python
  if (n==1 or n==2) : return 1;     # final de recorrencia
  return fibRec(n-1) + fibRec(n-2); # senao devolve

def main () :
  n = int(input());

  tempo_inicial = time.time(); # "dispara o cronometro"...
  fibA = fib(n);
  tempo_final = time.time();
  print("Iterativo: %3i - %3i em %f segundos" %
        (n, fibA, (tempo_final - tempo_inicial)));

  tempo_inicial = time.time(); # "dispara o cronometro"...
  fibA = fibRec(n);
  tempo_final = time.time();
  print("Recursivo: %3i - %3i em %f segundos" %
        (n, fibA, (tempo_final - tempo_inicial)));

main();

Se desejar tentar resolver o problema das Torres de Hanói seguir este apontador.

A. Por que o código da tabela 1 (seção P.A. de razão 1) não precisa de else?
Note que traduzindo os comandos da função somaRec para o Portugol, ele seria:
    se (n==0) devolva 0; //# final de recorrencia
    devolva n + somaRec(n-1);
Assim, se a condição n==0 resultar verdadeiro, então o comando devolva 0 é executado, voltando para quem invocou somaRec(0) (que pode ser somaRec(1) ou a função main, se tinha sido digitado 0 para n). Desse modo, a única possibilidade do comando devolva n + somaRec(n-1) ser executado é n==0 resultar falso e portanto a reservada else é desnecessária.

Leônidas de Oliveira Brandão
http://line.ime.usp.br

Alterações:
2020/08/20: acertos no formato
2020/08/15: novo formato, pequenas revisões
2020/08/13: novo formato, pequenas revisões
2020/06/18: novas imagens "img/img_fatorial_def.png" e "img/img_fatorial_fat3.png"; nova seção "Exemplo inicial de função recursiva"
2019/06/03: extensáo da seção "Exemplo de função ou definição recursiva";
2018/06/18: nova seção "como gerar binários";
2018/06/03: acrescentado versoes 'fatRecDepuracao(...)';
2018/06/03: versao inicial