Por que evitar entrada/saida de dados em funções

A razão principal para se evitar comandos de entrada e de saída dentro da definição de uma função é conseguir maior flexibilidade para uso dessas funções, como explico a seguir. Evidentemente isso não se aplica quando a função for desenhada especificamente para providenciar a entrada (leitura) ou para a saída (impressão de dados. Por exemplo, o segundo caso ocorre na função imprime_comb Entretanto, Para explicar as razões pelas quais deve-se evitar comandos de entrada e de saída dentro da definição de uma função, devemos primeiro enfatizar o que é a uma função em linguagens como C ou Python:

• é um código que recebe seus dados de entrada a partir de uma lista de parâmetros (parâmetros formais);
• é um código que processa os dados de entrada e geralmente devolve algum valor como resposta (em seu comando return);
• é um código que pode ser invocado a partir de outros trechos do programa, que providenciam os valores para os parâmetros (parâmetros efetivos).

Desse modo, usando como exemplo a função fatorial (fat(0)=1 e fat(n)=n*fat(n-1), n>0), a razão para se evitar comandos de entrada e de saída dentro da definição da função pode ser resumida em:

• Facilita o reúso de código, ou seja, sempre que precisar de um algoritmo que compute o fatorial, basta copiar o código que já implementou (e testou);
• Facilita o desenvolvimento de programas maiores, pois pode-se agrupar os blocos lógicos que tenham um propósito bem definido como uma função.

A fim de ficar mais clara a vantagem de passar os valores via parâmetro, vamos examinar um exemplo matemático, computar o número de combinações de n, tomados k a k [1]. Vamos lembrar a combinatória usualmente estudada no Ensino Médio. Este problema pode ser traduzido em um exemplo do tipo "loteria": de quantas maneiras distintas é possível combinar n=99 números (dentre 01 e 99) tomando-se k=5 deles? A resposta geral é dada pela expressão C_n,k=n!/((n-k)!k!), que com os dados de interesse resultaria em C_100,5=100!/((100-5)!5!) = 75.287.520.
Portanto, se você comprar um único bilhete dessa loteria por semana, em média precisaria de mais de 75 milhões de semanas para conseguir ter um bilhete premiado.
Como seria dificílimo tentar enumerar as mais de 75 milhões de possibilidade para verificar a corretuda da fórmula acima estão corretos, vamos testar com uma combinção menor, como combinar n=5 valores 3 a 3, neste caso a fórmula diz que teríamos
        C_5,3=5!/((5-3)!3!) = 5*4/2 = 10
e, de fato, existem 10 combinações: {1,2,3}, {1,2,4}, {1,2,5}, {1,3,4}, {1,3,5}, {1,4,5}, {2,3,4}, {2,3,5}, {2,4,5}, {3,4,5}.

Nesse contexto, imaginemos o uso errôneo de uma leitura do valor n dentro da função fat. Então, se precisar computar a combinação de n, tomados k a k (C_n,k=n!/((n-k)!k!)), esse valor não poderá ser computado usando a expressão seguinte (com chamada à função fat): fat(n)/(fat(n-k)fat(k)).
Por que mesmo?
Se não percebe o erro de programação, vale a pena fazer uma simulação. Suponha que você tenha implementado o fatorial como uma função com comando de leitura, em "Portugol"
    inteiro fat (n) { inteiro i=2, f=1; leia(n); repita_enquanto (i<=n) { f = f*i; i = i+1; } devolva f; }
e deseje saber C_5,2=5!/((5-2)!2!).
Então, ao entrar na função para computar fat(5) o usuário terá que digitar o valor 5, para computar fat(3), será obrigado a digitar o valor 3 e, para computar fat(2), terá também que digitar o valor 2.
Mas vamos tornar o erro (ou problema) mais óbvio. Vamos supor que desejamos imprimir várias combinações (e.g., para computar o triângulo de Pascal). Por exemplo, examine como ficaria o calculo de C_10,1, C_10,2, assim por diante até C_10,10 (vide a função fat da tabela 1). Seria necessário que o "sofrido" usuário tenha que ficar digitando 10 triplas! (10,9,1; 10,8,2; 10,7,3; 10,6,4; 10,5,5; 10,4,6; 10,3,7; 10,2,8; 10,1,9; e 10,0,10). Mas bastaria exigir que o usuário digitasse apenas um valor, 10, se o programador (você) tivesse implementado o fatorial via parâmetro e sem leituras dentro dessa função. Bastaria usar um laço (vide a função main da tabela 3).
Ou seja, não faz sentido obrigar o usuário a digitar dezenas, centenas, milhares, ou mais vezes, quando bastaria digitar um único valor. Se não estiver convencido da inviabilidade do uso de leitura dentro da função fatorial, copie os códigos da tabela 1 e o experimente.

Assim, em exercícios que apresentam o conceito de função (portanto envolvendo um bloco lógico com propósito bem definido), procure, sempre que possível, não usar comandos de entrada ou de saída de dados dentro da função. Esse é um bom hábito de programação, no sentido de reduzir erros e facilitar que reaproveite sues códigos em outras situações.
Mas vale lembrar que existem exceções: em uma função desenhada especificamente para "ler" dados, é necessá comandos para entrada e uma função específica para imprimir o Triângulo de Pascal precisa de comando de impressão.

Entretanto, existem as exceções, exemplos nos quais é útil usar comando de entrada ou de saída dentro da função. Ilustraremos o caso de utilidade de um comando de saída dentro da função, isso ocorre se desejamos computar (e imprimir) os n primeiros termos da sequência de Fibonacci. Então, naturalmente precisaremos do comando de impressão/saída e como isso pode ser feito para qualquer n é adequado agrupar esse código na forma de um procedimento separado (no caso uma função sem valor de retorno).
Porém se o objetivo fosse conhecer apenas o termo n da sequência, a função não deveria ter o comando de saída.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
20

int fat (int n) { // define funcao com 1 parametro
  int ft = 1, i=2;
  // Experimente com esta linha,
  scanf("%d", &n); // depois sem ela
  while (i <= n) {
    i = i + 1;
    ft = ft * i;
    }
  return ft;
  }
void imprime_comb (int n) {
  int i=0, aux;
  // Com mais a leitura abaixo o codigo ficaria
  // scanf("%d", &n); // "absurdo" ao quadrado!
  while (i <= n) {
    aux = fat(n)/(fat(n-i)*fat(i));
    printf("%3d ", aux);
    i++;
    }
  printf("\n");
  }
void main (void) {
  int i=0, n;
  // Experimente com n pequeno, digamos n=3, assim ja'
  scanf("%d", &n); // percebera' o absurdo da leitura
  while (i<=n) {
    imprime_comb(i);
    i++;
    }
  }

# Python2 para 'print' sem pular linha : print("*" , end = "");
from __future__ import print_function

def fat (n) :
  # Experimente com esta linha,
  n = int(input()); # depois sem ela
  f = 1;
  i = 2;
  while (i<=n) :
    f *= i;
    i += 1;
  return f;

def imprime_comb (n) :
  # Com mais a leitura abaixo o codigo ficaria
  # n = int(input()); # "absurdo" ao quadrado!
  i=0;
  while (i<=n) :
    # C(n,k) = n!/((n-k)!*k!)
    val = fat(n)/(fat(n-i)*fat(i));
    # print("C(%d,%d)=%d" % (n,i,val));
    print("%3d " % (val), end="");
    i += 1;

def main () :
  n = int(input());
  for i in range(n+1) :
    imprime_comb(i);
    print();

main();

Suponha que precisemos fazer um programa para computar quantas são as combinações de n termos combinados k-a-k, ou seja, tendo n elementos, desejamos saber de quantos modos distintos podemos formar grupos com k dos elementos.

Esse conceito aparece em probabilidade e em combinatória, sabemos que esta combinação corresponde ao agrupamentos de elementos nos quais a ordem não importa (tanto faz a ordem dos k elementos do tipo a) e que a fórmula que fornece o total desses subconjuntos é a seguinte:

Por exemplo, combinar 6 valores distintos, tomados 2 a 2 resulta 15=6!/((6-2)!2!)=6!/(4!2!), que são os 15 subconjuntos: (6,5), (6,4), (6,3), (6,2), (6,1), (5,4), (5,3), (5,2), (5,1), (4,3), (4,2), (4,1), (3,2), (3,1), (2,1).

Assim, existem duas possibilidades de implementar esse código, uma implementando a função fatorial (fat(n)) que seria invocada três vezes pelo programa principal (com algo como imprima(fat(n) / (fat(k) * fat(n-k)). Outra possibilidade é implementar também o cômputo de fat(n) / (fat(k) * fat(n-k)) também como uma função. Apesar dessa segunda possibilidade não ajudar tanto na organização do código (pois a segunda função (comb(n,k)) seria muito simples, ilustraremos dessa forma por ela usar função chamando função que chama função (a principal chama comb(n,k) e essa chama fat(n)). Veja como ficaria o código em uma pseudo-linguagem de programação:

inteiro fat(n) { //# estou supondo que o valor digitado pelo usuario seja um natural maior ou igual a 0 (n>=0)
  inteiro valfat = 1;
  inteiro cont = 2;
  repita_enquanto (cont<=n) { //# continue computando enquanto nao chegar ao valor cont==n
    valfat = valfat * cont;
    cont = cont + 1;
    }
  devolva valfat;
  }
inteiro comb(n, k) {
  devolva fat(n) / (fat(n-k)*fat(k));
  }
vazio principal() {
  inteiro N, k; //# note que os nomes de variaveis daqui NAO tem qualquer relacao com aqueles em 'fat'
  inteiro a, b, c; //# para uma segunda versao
  leia(N, k); //# leia 2 valores naturais e armazene-os respectivamente em N e em k (espera-se que digite N>=k)
  //# pode-se invocar seguidamente 'fat' 3 vezes como abaixo:
  imprima(comb(N,k);
  //# pode-se invocar a funcao 'fat' quanta vezes forem necessarias, aqui fazermos 3 vezes, armazenando cada resultado
  a = fat(N);
  b = fat(k);
  c = fat(N-k);
  imprima(a/( b * c))); //# usamos os 3 resultados de chamada de 'fat' para compor a resposta final N!/(k!*(N-k)!)
  }

A figura 1 ilustra os desvios no fluxo de execução do código acima. Note o destaque da instrução 2, que é uma atribuição que define o valor para a variável c, a ordem de construção é a usual de expressão, primeiro computa-se o lado direito da expressão e o resultado dela é armazenado na variável (que é o lado esquerdo da atribuição). Como o lado direito contém uma chamada de função, para computá-lo, desvia-se o fluxo de execução (seta que "sai" de fat(k);) para a execução da função fat(.), inicia-se a variável local (na verdade declarada como parâmetro) n com o valor vindo de k (parâmetro efetivo), segue-se executando as instrução de fat(.) e, no exemplo, a última instrução indica que deve-se devolver para local que invocou fat(.) o valor atual na variável (local) ft.

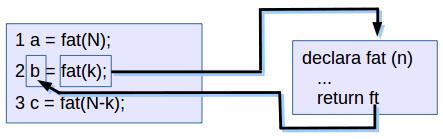
Fig. 1. Diagrama esquemática indicando desvio de execução função e local de retorno.

Novamente para enfatizar as desvantagens de usar leitura ou impressão dentro de funções, procure implementar o código acima, em sua linguagem favorita, e colocar nele comandos para leitura ou saída dentro da função fat(n), como discutido abaixo.

Note que, se dentro da função fat exitisse um comando do tipo leia(n);, a função NÃO poderia ser usada para computar o fatorial de algum valor já registrado em alguma variável, pois ao ser invocada, digamos fat(n), seria necessário que o usuário digitasse novamente o valor para calculo do fatorial e valor para o qual desejava-se o fatorial (na variável n) seria descartado. No exemplo do código associado à figura 1, na primeira chamada para N, o usuário teria que digitar algum valor para calcular fatorial (e provavelmente nem saberia qual o valor guardado em N), na segunda chamada, para o valor para k ocorreria o mesmo, e por fim, o mesmo para o valor N-k.

De forma análoga, se a função fat tivesse algum comando de saída, ao usar a função 3 vezes, o usuário receberia informações confusas: ele deseja a combinação de n, tomado k-a-k, mas receberia 4 infomações: na primeira chamada fat(.) imprimiria n!, segunda imprimiria k!, na terceira imprimiria o resultado de (n-k)! e, ao voltar para o código que invocou fat(.), imprimiria finalmente a única coisa que o usuário desejava saber, n!/(k! (n-k)!).

Vamos aproveitar o código que computa a combinação de n, k-a-k, C(n,k) = n!/(k!*(n-k)!), para computar a seguinte sequência de valores: C(n,0), C(n,1), C(n,2) e assim por diante, até C(n,n). Mais ainda, vamos fazer isso para n=1, n=2, n=3 e n=4.

Linha | Combinacoes C(n,0) ate C(n,n)                         | As saidas
    0 | C(0,0)                                                |   1
    1 | C(1,0) C(1,1)                                         |   1   1 
    2 | C(2,0) C(2,1) C(2,2)                                  |   1   2   1 
    3 | C(3,0) C(3,1) C(3,2) C(3,3)                           |   1   3   3   1 
    4 | C(4,0) C(4,1) C(4,2) C(4,3) C(4,4)                    |   1   4   6   4   1 
    5 | C(5,0) C(5,1) C(5,2) C(5,3) C(5,4) C(5,5)             |   1   5  10  10   5   1 
    6 | C(6,0) C(6,1) C(6,2) C(6,3) C(6,4) C(6,5) C(6,6)      |   1   6  15  20  15   6   1

Ou seja, na tabela acima, a linha 0, tem uma única saída, a saber C(0,0). A linha 1 tem duas saídas, C(1,0) e C(1,1). A linha 2 tem três saídas, C(2,0), C(2,1) e C(2,2). Assim, por diante, até a linha 6 que tem sete saídas.

O que é interessante, é que no triângulo (na coluna das saídas) aparece uma propriedade interessante: o elemento da linha k, na coluna j é igual à soma do elemento da linha k-1, na coluna j-1, com o elemento da linha k-1, na coluna j. Ou seja, vale a propriedade C(k,j) = C(k-1,j-1) + C(k-1,j) (sempre que k>0 e j estiver entre 1 e k, essa é a relação de Stifel [2, 3], e aquele é o Triângulo de Pascal. Veja por exemplo o Triângulo de Pascal [2] na WikiPedia.

Abaixo apresento uma implementação para gerar o "Triângulo de Pascal" (como apresentado acima), nas linguagens C e Python.

#include <stdio.h>
int fat (int n) { // supondo usuario digite natural n>=0)
  int valfat = 1;
  int cont = 2;
  while (cont<=n) { // continue enquanto nao chegar a cont==n
    valfat = valfat * cont;
    cont++;
    }
  return valfat;
  }

int comb (int n, int k) { return fat(n) / (fat(n-k)*fat(k)); }

void main (void) {
  int N, k; //  usa inteiros N, k
  int a, b, c, n;
  printf("Digite N - para computar C(N,0), C(N,1), ..., C(N,N): ");
  scanf("%d",  &N);
  // pode-se invocar seguidamente 'fat' 3 vezes como abaixo:
  for (n=0; n>N; n++) {
    for (k=0; k<=n; k++) {
      a = fat(n);
      b = fat(k);
      c = fat(n-k);
      // usamos resultados de 'fat' para resposta N!/(k!*(N-k)!)
      printf("%3d ", a/(b * c));
      }
    printf("\n");
    }
  }

# Python2 para 'print' sem pular linha : print("*" , end = "");
from __future__ import print_function

def fat (n) : # supondo usuario digite natural n>=0)
  valfat = 1;
  cont = 2;
  while (cont<=n) : # continue enquanto nao chegar a cont==n
    valfat = valfat * cont;
    cont = cont + 1;
  return valfat;

def comb(n, k) :
  return fat(n) / (fat(n-k)*fat(k));

def main () :
  # usa inteiros N, k
  print("Digite N - para computar C(N,0), C(N,1), ..., C(N,N): ");
  N = int(input());
  # pode-se invocar seguidamente 'fat' 3 vezes como abaixo:
  for n in range(N) :
    for k in range(n+1) :
      a = fat(n);
      b = fat(k);
      c = fat(n-k);
      # usamos resultados de 'fat' para resposta N!/(k!*(N-k)!)
      print("%3d " % (a/(b * c)), end="");
    print();

main();

1. [1] https://en.wikipedia.org/wiki/Binomial_coefficient.
2. [2] Uta C. Merzbach e Carl B. Boyer, "A History of Mathematics", third edition, John Wiley & Sons, Inc., 2011 (primeira edicao de 1968)
3. [3] Tobias Dantzig, "NUMBER: The Language of Science", Pi Press, New Yourk, 2005

Leônidas de Oliveira Brandão
http://line.ime.usp.br

Alterações:
2020/08/09: revisão do formato e ampla revisão do texto;
2019/06/06: vários pequenos acertos ao longo do texto;
2019/04/07: versao 2 (acrescentado novos paragrafos, melhorando explicacoes e frases);
2017/04/06: primeira versao.