[
Fatorial |
Depurando fatorial |
Busca Binária |
Depurando a Busca Binária
]
Introdução aos algoritmos recorrentes/recursivos: alguns exemplos
Nesta seção examinaremos alguns exemplos de algoritmos recorrentes (ou recursivos).
A apresentação do conceito pode ser encontrada
nesta página.
Fatorial implementado de modo recursivo
A função matemática fatorial descreve o númeto de permutações distintas de um conjunto finito.
Sua definição é intrinsecamente recursiva:
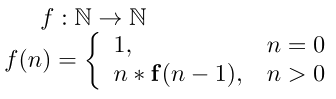
Em termos práticos a função fatorial pode ser implementada como indicado abaixo, utilizando
recorrência de cauda, ou seja, a chamada recursiva corresponde às últimas instruções da função.
| Função fatorial implementada recursivamente |
|---|
| C | Python |
|---|
#include <stdio.h>
// Fatorial recursivo
int fatRec (int n) {
if (n==0) return 1; // final de recorrencia
return n * fatRec(n-1); // senao devolve n x "o fatorial de n-1" (inducao)
}
int main (void) {
int n;
scanf("%d", &n);
printf("O fatorial de %d e': %d\n", n, fatRec(n));
return 1;
} |
|
# Fatorial recursivo
def fatRec (n) : # os finalizadores ';' sao opcionais em Python
if (n==0) : return 1; # final de recorrencia
return n * fatRec(n-1); # senao devolve n x "o fatorial de n-1" (inducao)
def main () :
n = int(input());
print("O fatorial de %d e': %d" % (n, fatRec(n)));
main();
|
A execução de uma função recursiva é realizada empilhando-se o contexto de execução,
de modo que no momento que a chamada recursiva termina, retorna-se ao contexto empilhado e,
ao finalizado a chamada "inicial", o contexto é removido da pilha (desempilhado).
Em detalhes, vejamos uma simulação da função fatRec acima apresentada para n=3.
Ord. n Imprimir (esquema de execução)
1 3 fatRec(3)
2 2 fatRec(3) = 3*fatRec(2) -> fatRec(2)
3 1 ^ ^ 2*fatRec(1) -> fatRec(1)
4 0 | | ^ 1*fatRec(0) --> fatRec(0)
| | | ^
| | | |
5 0 | | | +-- 1 .. final desse contexto n=0
6 1 | | +--------- 1 = 1*1 .... final do contexto 'fatRec(1)'
7 2 | +--------- 2 = 2*1 .................. final do contexto 'fatRec(2)'
8 3 +------ 6 = 3*2 ................................... final do contexto 'fatRec(3)'
|
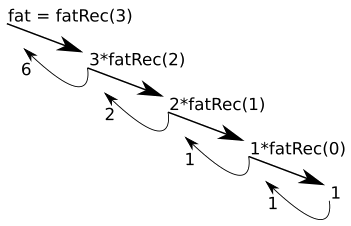 |
Na primeira coluna, sob rótulo
Ord., está o tempo de execução, sendo os números a ordem de execução dos
comandos. Na segunda coluna está o valor do
n no contexto da chamada sendo simulada.
Note que na ordem de cada instrução, separamos o comando k * fatRec(k-1) em duas instruções,
primeiro obter o valor de fatRec(k-1), digamos FK, e depois a instrução k * FK.
Um exemplo mostrando o comportamento da função recursiva
Podemos alterar o código da função recursiva fatRec acima para percebermos mais claramente
os contextos de execução e os níveis de recorrência.
Por nível de recorrência deve-se entender o número de vezes que a recorrência é invocada, por exemplo,
para n=0, teremos nível de recorrência 0, para n=1, nível 1 e assim por diante.
Abaixo os códigos em C e em Python, imprimindo a chegada ao contexto n, deslocando-se
horizontalmente a impressão de acordo com o nível da recorrência ("indentação").
Por essa razão, precisaremos passar um parâmetro adicional, que sempre terá o valor inicial do n.
| Função fatorial implementada recursivamente |
|---|
| C | Python |
|---|
#include <stdio.h>
char brancos[] = " ";
int fatRec (int N, int k) {
int aux;
printf("%*.s", 2*(N-k), brancos); // truque: nivel rec. maior => deslocar mais
printf("Entrei em fat(%d)\n", k);
if (k==0) aux = 1; // final de recorrencia
else aux = k * fatRec(N, k-1); // senao devolve k x "o fatorial de k-1"
printf("%*.s", 2*(N-k), brancos);
printf("Saindo de fat(%d): devolve %d\n", k, aux);
return aux;
}
int main (void) {
int n, fat;
scanf("%d", &n);
printf("Antes de iniciar chamada a fat(%d)\n", n);
fat = fatRec(n, n);
printf("Apos chamada a fat(%d)\n", n);
return 1;
} |
|
from __future__ import print_function; # para Python 2
# Fatorial recursivo
def fatRec (N, k) : # os finalizadores ';' sao opcionais em Python
print((N-k) * " ", end=""); # truque: nivel rec. maior => deslocar mais
print("Entrei em fat(%d)" % k);
if (k==0) : aux = 1; # final de recorrencia
else : aux = k * fatRec(n, k-1); # senao devolve k x "o fatorial de k-1"
print((N-k) * " ", end=""); # truque: nivel rec. maior => deslocar mais
print("Saindo de fat(%d): devolve %d" % (k, aux));
return aux;
def main () :
n = int(input());
print("Antes de iniciar chamada a fat(%d)" % n);
fatRec(n, n);
print("Apos chamada a fat(%d)" % n);
main();
|
Assim, se rodarmos qualquer uma das versões para n=3, teremos a seguinte impressão:
Antes de iniciar chamada a fat(3)
Entrei em fat(3)
Entrei em fat(2)
Entrei em fat(1)
Entrei em fat(0)
Saindo de fat(0): devolve 1
Saindo de fat(1): devolve 1
Saindo de fat(2): devolve 2
Saindo de fat(3): devolve 6
Apos chamada a fat(3) |
 |
Outro exemplo de recursividade em C e em Python: busca binária
Se analisarmos a frequência de uso dos variados tipos de algoritmo, provavelmente o campeão de uso
é a busca de elemento em vetor/lista/conjunto.
Para que essa busca seja eficiente, geralmente mantemos os dados ordem (e.g., crescente), assim
podemos empregar um algoritmo de busca muito rápido, a busca binária.
A busca binária é feita sobre listas ordenadas, adotando o seguinte esquema:
1. busca(vet, x, ini, fim) // busca o elemento x em vet entre as posições ini e fim;
2. se (ini > fim), então devolva que não existe mais intervalo onde procurar
3. meio = (ini + fim) / 2; // usando a divisão inteira
4. se (vet[meio] == x), então devolva que encontramos na posição meio
5. se (vet[meio] < x), então x não pode estar na primeira metade, busque entre meio+1 e fim
6. se (vet[meio] > x), então x não pode estar na segunda metade, busque entre ini e meio-1
Note que na descrição acima, o algoritmo é naturalmente recursivo, então faremos essa implementação em
C e em Python.
| Busca binária implementada recursivamente |
|---|
| C | Python |
|---|
int busca (int vet[], int x, int ini, int fim) { // busca x entre vet[ini] e vet[fim]
int meio;
if (ini>meio) return -1; // nao tem mais onde procurar!
meio = (ini+fim) / 2; // pegar indice do elemento do meio
if (vet[meio]==x)
return meio; // encontrei na posicao meio
else
if (vet[meio] < x) // vet[ini]...vet[meio] NAO contem x
// entao busque (recursivamente) entre vet[meio+1] e vet[fim]
return busca(vet, x, meio+1, fim);
else // vet[meio]...vet[fim] NAO contem x
// entao busque (recursivamente) entre vet[ini] e vet[meio-1]
return busca(vet, x, ini, meio-1);
} // nunca executaria esta linha - por que? |
|
def busca (vet, x, ini, fim) : # busca x entre vet[ini] e vet[fim]
if (ini>meio) : return -1; # nao tem mais onde procurar!
meio = (ini+fim) / 2; # pegar indice do elemento do meio
if (vet[meio]==x) :
return meio; # encontrei na posicao meio
elif (vet[meio] < x) : # vet[ini]...vet[meio] NAO contem x
# entao busque (recursivamente) entre vet[meio+1] e vet[fim]
return busca(vet, x, meio+1, fim);
else : # vet[meio]...vet[fim] NAO contem x
# entao busque (recursivamente) entre vet[ini] e vet[meio-1]
return busca(vet, x, ini, meio-1);
# nunca executaria esta linha - por que?
|
Simulando e depurando a busca binária
Da mesma forma que inserimos várias linhas de impressão para ajudar a entender as recorrência na
função fatorial, inclusive usando um truque para visualizar o nível da recorrência,
faremos o mesmo com o algoritmo de busca binária.
| Busca binária recursiva com mensagens para visualizar nível de recorrência |
|---|
| C | Python |
|---|
// busca x entre vet[ini] e vet[fim]
int busca (int vet[], int x, int ini, int fim, int N, int k) {
int meio = (ini+fim) / 2; // pegar indice do elemento do meio
printf("%*.s", 2*(N-k), brancos); // para fazer indentacao
printf("Entrei em busca(%d,%d): meio = %d\n", ini, fim, meio);
if (ini > meio) {
printf("%*.s", 2*(N-k), brancos);
printf("Nao ha mais onde buscar: %d > %d)\n", ini,fim);
return -1; // nao tem mais onde procurar!
}
if (vet[meio]==x) {
printf("%*.s", 2*(N-k), brancos);
printf("Achei %d na posicao %d!\n", x, meio);
return meio; // encontrei na posicao meio
}
else
if (vet[meio] < x) { // vet[ini]...vet[meio] NAO contem x
printf("%*.s", 2*(N-k), brancos);
printf("Busque na segunda metade: %d e %d\n", meio + 1, fim);
// entao busque (recursivamente) entre vet[meio+1] e vet[fim]
return busca(vet, x, meio+1, fim, N, k-1);
}
printf("%*.s", 2*(N-k), brancos);
printf("Busque na primeira metade: %d e %d\n", ini, meio - 1);
// entao busque (recursivamente) entre vet[ini] e vet[meio-1]
return busca(vet, x, ini, meio-1, N, k-1);
}
int main (void) {
int vet[] = { -1, 0, 3, 3, 5, 6, 7, 8, 9 };
int n = 9, resp;
//int x = 7; // buscar 7
int x = 2; // buscar 2
printf("Antes de iniciar chamada a busca(%d)\n", x);
resp = busca(vet, x, 0, n, n, n);
printf("Apos chamada a busca(%d)\n", x);
if (resp>-1) printf("Encontrei em %d: de fato %d = %d\n", resp, x, vet[resp]);
else printf("NAO encontrei %d\n", x);
return 0;
} |
|
# busca x entre vet[ini] e vet[fim]
def busca (vet, x, ini, fim, N, k) :
global conta;
conta += 1;
if (conta>10) : return -1;
meio = (ini+fim) / 2; # pegar indice do elemento do meio
print((N-k) * " ", end=""); # truque: nivel rec. maior => deslocar mais
print("Entrei em busca(%d,%d): meio = %d" % (ini,fim, meio));
if (ini>meio) :
print((N-k) * " ", end=""); # truque: nivel rec. maior => deslocar mais
print("Nao ha mais onde buscar: %d > %d)" % (ini,fim));
return -1; # nao tem mais onde procurar!
if (vet[meio]==x) :
print((N-k) * " ", end="");
print("Achei %d na posicao %d!" % (x,meio));
return meio;
elif (vet[meio] < x) : # vet[ini]...vet[meio] NAO contem x
print((N-k) * " ", end="");
print("Busque na segunda metade: %d e %d" % (meio + 1, fim));
# entao busque (recursivamente) entre vet[meio+1] e vet[fim]
return busca(vet, x, meio+1, fim, N, k-1);
else : # vet[meio]...vet[fim] NAO contem x
print((N-k) * " ", end="");
print("Busque na primeira metade: %d e %d" % (ini, meio - 1));
# entao busque (recursivamente) entre vet[ini] e vet[meio-1]
return busca(vet, x, ini, meio-1, N, k-1);
def main () :
vet = [ -1, 0, 3, 3, 5, 6, 7, 8, 9 ];
n = len(vet);
#x = 7; # buscar 7
x = 2; # buscar 2
print("Antes de iniciar chamada a busca(%d)" % x);
resp = busca(vet, x, 0, n, n, n);
print("Apos chamada a busca(%d)" % x);
if (resp>-1) : print("Encontrei em %d: de fato %d = %d" % (resp, x, vet[resp]));
else : print("NAO encontrei %d" % x);
main();
|
Procure criar uma função recursiva, eventualmente com mais de uma chamada como é o caso da
função de busca binária acima, com as mensagens e usando o truque para fazer indentação.
Então procure simular manualmente sua função, depois rode sua implementação e veja se
o resultado foi o esperado.
Cuidado com recorrência infinita (que equivale a laça infinito), por exemplo, utilize
uma variável global conta=0 e dentro de sua função, use como primeira linha
algo como
conta += 1; if (conta>20) return -1;
(no Python lembre-se de declarar como global com a linha: global conta).
Leônidas de Oliveira Brandão
http://line.ime.usp.br
Alterações:
2020/08/15: novo formato, pequenas revisões
2020/08/13: novo formato, pequenas revisões
2020/06/18: nova imagem "img/img_fatorial_def.png" e "img/img_fatorial_fat3.png";
2019/06/03: extensáo da seção "Exemplo de função ou definição recursiva";
2018/06/15: primeira versão.