Introdução aos números em ponto flutuantes

Nesta seção examinaremos resumidamente como o computador representa números reais. A seção seguinte foi redigida para aqueles que desejam conhecer mais, estudando-a pode-se compreender a matemática associada ao conteito de representação de números em um computador digital e a razão do termo ponto flutuante.

Normalmente deve-se utilizar um número fixo de bits para representar cada número. Por exemplo, se determinado computador usar apenas 2 bytes (ou 16 bits) para representar um real e convencionar-se que o primeiro byte armazena a parte inteira e o segundo byte a parte decimal, teríamos uma variabilidade pequena de números. Como visto no texto introdutório sobre inteiros, com 8 bits, teríamos (simplificadamente) desde o 11111111 (primeiro bit indica negativo) até o 01111111, que em decimal seriam desde -127 até o 127, pois

1111111₂ = 2⁷ + 2⁶ + 2⁵ + 2⁴ + 2³ + 2² + 2¹ + 2⁰ = 128 + 64 + 32 + 16 + 8 + 4 + 2 + 1 = 255 (1)

Um primeiro modelo (ineficiente) para representar valores reais: ponto fixo

Para apresentar o conceito que interessa, de ponto flutuante, apresentarei sua contra-parte, como seria uma representação em ponto fixo. Vamos continuar usando 2 bytes (logo 16 bits) e considerar 3 agrupamentos: P1. o primeiro bit para representar o sinal do número (s=0 para positivo e s=1 para negativo); P2. os próximos 7 como a parte "decimal" (após vírgula decimal); e P3. os últimos 8 bits para o valor inteiro do número.

Assim, para obter o maior valor positivo que poderia ser representado nesta notação, deveríamos deixar o primeiro bit em zero (para ser positivo) e todos os seguintes "ligados": 0 1111111 11111111 (deixei espaço em branco para indicar os 3 agrupamentos).
Assim, a parte "decimal" P2 (1111111) corresponde em decimal:

2^-1 + 2^-2 + 2^-3 + 2^-4 + 2^-5 + 2^-6 + 2^-7 = 0.5 + 0.25 + 0.125 + 0.0625 + 0.03125 + 0.015625 + 0.007812 = 0.992188 (2)
Portanto o maior positivo, convertendo para decimal, seria a soma de (1) e (2): 255.992188. Desse modo, em ponto fixo:
Tab. 1. Maior e menor positivo que pode-se obter com a representação em ponto fixo

- maior valor positivo em binário 00111111 01111111₂ = 255.992188 em decimal;
- menor valor estritamente positivo em binário 00000001 00000000₂ = 0.007812 em decimal.

Um modelo de representação para real mais eficiente: ponto flutuante

Uma alternativa mais eficiente e amplamente utilizada na prática é a representação em ponto flutuante. Nessa representação também quebramos o número em três agrupamentos, a primeira sendo o sinal s, a segunda o expoente e e a terceira sendo mantissa m, assim o valor do número seria s x m x b^e. Se a mantissa tiver p dígitos, o número é: s x d₀d₁...d_p-1 x b^e.

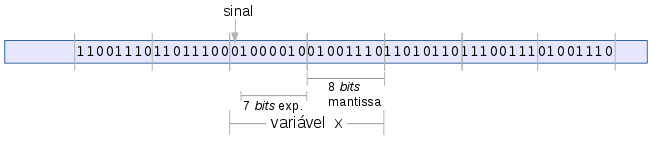
Fig. 1. Representação em memória para ponto fixo para representar reais, com 7 bits de expoente e 8 bits para mantissa.

Assim, nota-se que a diferença entre a representações em ponto flutuante e em ponto fixo é o tratamento do segundo agrupamento. Para poder comparar ambas as representações, vamos novamente supor um computador com reais usando apenas 2 bytes.

Desse modo, o maior real positivo nesse ponto flutuante é obtido usando a maior potência e maior mantissa possiveis, respectivamente 0111111 e 11111111, que em decimal são,
2⁶ + 2⁵ + 2⁴ + 2³ + 2² + 2¹ + 2⁰ = 64 + 32 + 16 + 8 + 4 + 2 + 1 = 127 (3)
2⁸ + 2⁷ + 2⁶ + 2⁵ + 2⁴ + 2³ + 2² + 2¹ + 2⁰ = 256 + 128 + 64 + 32 + 16 + 8 + 4 + 2 + 1 = 511 (4)
Portanto, o maior real positivo nesse ponto flutuante é 511 x 2¹²⁷, um número gigantesto (maior que 1.70141183 x 10³⁸).

De forma análoga, podemos computar o menor valor estritamente positivo que conseguimos com essa representação. Como são 7 bits para expoente e 8 bits para a mantissa, devemos pegar no agrupamento P2 a sequência 1111111 (maior potência negativa possível) e no agrupamento P3 o menor valor positivo, que seja maior que zero, portanto 00000001. Convertendo 1111111 para decimal, temos o valor -64, logo o menor positivo é: 2^-64 que é aproximadamente 5.42101086243e-20 (tremendamente pequeno).

Portanto o maior positivo e o menor , convertendo para decimal, seria a soma de (1) e (2): 255.992188. Desse modo, em ponto fixo:
Tab. 2. Maior e menor positivo que pode-se obter com a representação em ponto flutuante

- maior valor positivo em binário 00111111 01111111₂ > 1.70141183 * 10³⁸ em decimal;
- menor valor estritamente positivo em binário 1111111 00000001₂ ~= 5.42101086243e-20 em decimal.

Comparando os resultados de ponto flutuante com ponto fixo, tabelas 1 e 2, percebemo que ponto flutuante produz resultados muito melhores em termos de capacidade de "simular" os números reais.

Representação em ponto flutuante

Esta técnica de representação é a mais utilizada nos computadores, ela utiliza um bit para sinal, uma quantidade pequena de bits para o expoente e uma quantidade maior de bits para a parte "principal" do número. Em um dos padrões de representação (IEEE 754) o número é representado com 11 bits para o expoente e 52 bits para a mantissa.

Exemplo de representação em ponto flutuante

Para ilustrar o funcionamento de ponto flutuante, suponha um computador que use representação em decimal (os computadores na verdade usam base binária), tendo apenas 3 dígitos para mantissa e o expoente sendo de -4 até -4, assim teríamos p=3 e -4<e<4.

Deste modo, o maior valor real que pode ser representado seria o 999000, pois tomando a maior mantissa e maior expoente, teríamos 10³ x 999 = 999000.

Já o menor valor estritamente positivo que conseguiríamos seria o 0.001, pois tomando a menor mantissa positiva e menor expoente possível (-3), teríamos 10^-3 x 1 = 0.001.

Desse modo, nesse computador simples, a variação de números "reais" que poderiam ser representados nesse computador, seria:
Tab. 3. Maior e menor positivo que pode-se obter com a representação em ponto flutuante em decimal.

- maior valor positivo: 999 x 10³ = 999000;
- menor valor estritamente positivo: 1 x 10^-3 = 0.001.

Erros numéricos

A primeira questão que aparece ao tratar números não inteiros no computador digital é a perda de precisão ou os erros numéricos. Por exemplo, mesmo em notação decimal o valor 1/3 não será representado perfeitamente, ele será registrado com algo semelhante a 0.3333 (se o computador utilizar 4 dígitos).

Um exemplo do problema numérico está ilustrado no exemplo abaixo, quando tentamos imprimir as somas de 0.1 até 0.9. Experimente copiar este trecho de código e roder em C ou em Python, você verá que o algoritmo nunca parará! Isso mesmo, laço infinito, pois como o computador utiliza notação binário e como o decimal 0.1 em binário corresponde a um binário periódico (como a dízima periódica resultante do 1/3 que é 0.3...).
Tab. 4. Cuidado com a aritmética de ponto flutuante! Nem tudo é o que parece ser...

C Python

x = 0.1; while (x!=1.0) { printf("%f\n", x); x += 0.1; } printf("Final!\n");

x = 0.1 while (x!=1.0) : print(x) x += 0.1 print("Final!")

Entrada e saída de flutuantes em C e em Python

Em C deve-se utilizar o formatador %f para indicar que os bits devem ser tratados como número em ponto flutuante, enquanto em Python deve-se utilizar a função float(...), como indicado no exemplo abaixo.
Tab. 5. Como imprimir números em ponto flutuante.

C Python

float x; // declaracao de variavel em "ponto flutuante" scanf("%f", &x); // leia como "ponto flutuante" printf("%f\n", x); // imprima como "ponto flutuante" // Usar formatador %N.kf para usar N posicoes ajustadas 'a direita e k decimais printf("Tab.\nx=%3.2f\nx=%3.2f", x, x); // imprima com 2 casas decimais

x = float(input()) # leia e transforme em "ponto flutuante" print(x); # impressao simples # Util para colocar frases mais "sofisticadas" print("x=%f - frases mais \"sofisticadas\"" % x); # impressoes mais sofisticadas # Assim e' util para construir tabelas. print("Tab.\nx=%3.2f\nx=%3.2f" % (x,x)); # o \n quebra linha

Aos alunos estudando com a linguagem C, tomem um cuidado adicional: o compilador C aceita utilizar o formatador de inteiro na leitura e na impressão de uma variável em flutuante. Ele trunca o valor, assim se tiver float x=1.5; e fizer printf("x=%d\n", x);, não haverá erro de compilação e será impresso x=1.

Uma boa fonte para pesquisar é examinar o texto na WikiPedia: floating-point.

Leônidas de Oliveira Brandão
http://line.ime.usp.br

Alterações:
2020/08/10: novas seções iniciais;
2020/04/18: inserido nomes nas tabelas, correcao tab. 1 ("x+=1.0"->"x+=0.1")
2017/04/14: primeira versão